Convolutional LSTM Network-- A Machine Learning Approach for Precipitation Nowcasting
论文地址:arxiv
摘要
作者将降水临近预报表述为一个时空序列预测的问题,其中输入和预测目标都是时空序列。通过将全连接 LSTM (FC-LSTM)扩展为在输入到状态到状态的转换中都具有卷积结构,提出了卷积 LSTM (ConvLSTM),将其用于构建一个端到端的可训练的降水临近预报模型。
正文
由于降水预报所需的预报分辨率与时间精度很高,所以成为一个热门研究课题。
对于降水临近预报的方法可以分为两类:一个是基于 NWP 的方法与基于雷达回波锁步操作的方法。现在的预报系统通常使用外推方法。
现在已经有深度学习的进展,尤其是循环神经网络与长短期记忆模型。作者改进了全连接 LSTM,将其扩展到 ConvLSTM,在输入到状态和状态到状态的转换中都有卷积结构。通过塕多个 ConvLSTM 层并形成编码-预测结构,作者可以构建一个端到端的可训练的降水临近预报模型。
预备知识
用于序列建模的长短期记忆网络
LSTM 的主要创新在于其记忆 $c_t$,该单元实质上充当状态信息的累加器。记忆单元通过几个自参数化的控制门访问,写入和清除。每次有新的输入时,如果输入门被激活,其信息将累加到记忆单元中。此外,如果遗忘门 $f_t$ 开启,过去的记忆单元状态 $c_{t-1}$ 可能会在此过程中被”遗忘”。最新的记忆单元输出 $c_t$ 是否会传播到最终状态 $h_t$ 进一步由输出门 $o_t$ 控制。其关键方程如下:
$$
i_t = σ(W_{xi}x_t + W_{hi}h_{t-1} + W_{ci} ◦ c_{t-1} + b_i)
$$
$$
f_t = σ(W_{xf}x_t + W_{hf}h_{t-1} + W_{cf} ◦ c_{t-1} + b_f)
$$
$$
c_t = f_t ◦ c_{t-1} + i_t ◦ tanh(W_{xc}x_t + W_{hc}h_{t-1} + b_c)
$$
$$
o_t = σ(W_{xo}x_t + W_{ho}h_{t-1} + W_{co} ◦ c_t + b_o)
$$
$$
h_t = o_t ◦ tanh(c_t)
$$
其中,$◦$ 表示 Hadamard 积。
模型架构
卷积长短时记忆网络(ConvLSTM)
全连接的 LSTM 对于空间数据而言有过多的冗余,作者提出了 ConvLSTM,其所有的输入 $X_1,…,X_t$,单元输出 $C_1,…,C_t$,隐藏状态 $H_1,…,H_t$ ,以及门控单元 $i_t,f_t,o_t$ 都是三维张量。其最后两个维度是空间维度(行与列)。
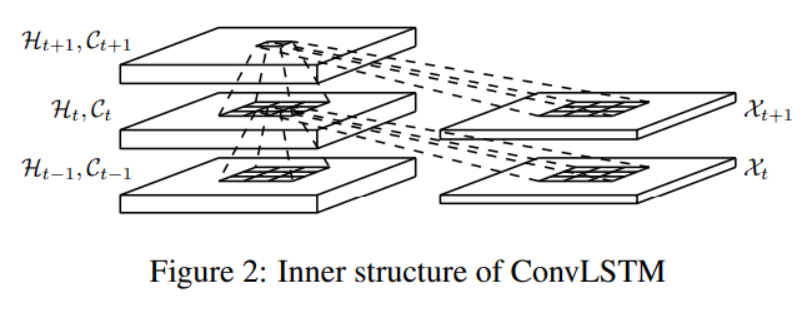
ConvLSTM输入和其局部邻居的过去状态来确定网格中某个单元的未来状态。为通过状态到状态的和输入到状态的转换中使用卷积运算符轻松实现。
其关键方程如下所示,其中,$*$ 表示卷积运算符,$◦$ 表示 Hadamard 积。
$$
\begin{align*}
i_t &= \sigma(W_{xi} * X_t + W_{hi} * H_{t-1} + W_{ci} \circ C_{t-1} + b_i) \
f_t &= \sigma(W_{xf} * X_t + W_{hf} * H_{t-1} + W_{cf} \circ C_{t-1} + b_f) \
C_t &= f_t \circ C_{t-1} + i_t \circ \tanh(W_{xc} * X_t + W_{hc} * H_{t-1} + b_c) \
o_t &= \sigma(W_{xo} * X_t + W_{ho} * H_{t-1} + W_{co} \circ C_t + b_o) \
H_t &= o_t \circ \tanh(C_t)
\end{align*}
$$
如果将状态视为运动物体的隐藏表示,那么具有较大转换核的 ConvLSTM 应该可以捕捉到更快的运动,而较小核可以捕捉到较慢的运动。
为了确保状态与输入具有相同的行数与列数,在应用卷积操作之前需要进行填充。在这里,边界点的隐藏状态填充可以被视为使用外部世界的状态进行计算。通过在第一个输入到来之前,会将所有 LSTM 的状态初始化为零,这对应于未来的完全无敌。
类似的,如果对隐藏状态进行零填充,实际上是将外部世界的状态设为零,并假设对外部没有先验知识。通过对状态进行填充,可以不同地处理边界点,这在许多情况下都是有帮助的。
编码-预测结构
对于时空序列预测问题,作者采用如下所示的结构,该结构由两个网络组成,编码网络与预测网络。
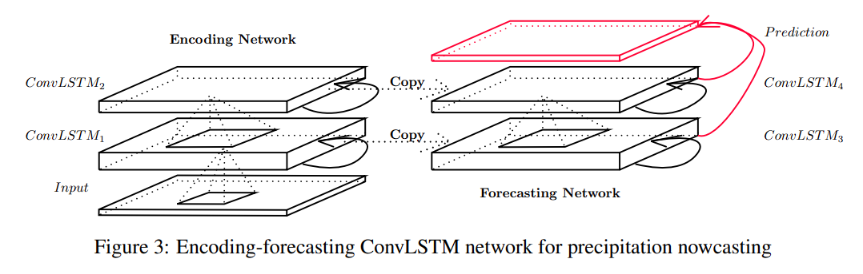
预测网络的初始状态与单元输出是从编码网络的最后状态复制出来的。这两个网络都是通过堆叠多个 ConvLSTM 层构成的。由于我们的预测目标与输入具有相同的维度,作者将预测网络中的所有状态连接起来,并将它们输入到一个 $1*1$ 的卷积层中,以生成最终的预测结果。
编码 LSTM 将整个输入序列压缩成一个隐藏状态张量,而预测 LSTM 则异形这个隐藏状态以给出最终的预测:
$$
\begin{align}
\tilde{X}{t+1}, \ldots, \tilde{X}{t+K} &= \arg \max_{X_{t+1}, \ldots, X_{t+K}} p(X_{t+1}, \ldots, X_{t+K} \mid \hat{X}{t-J+1}, \hat{X}{t-J+2}, \ldots, \hat{X}{t}) \
&\approx \arg \max{X_{t+1}, \ldots, X_{t+K}} p(X_{t+1}, \ldots, X_{t+K} \mid f_{\text{encoding}}(\hat{X}{t-J+1}, \hat{X}{t-J+2}, \ldots, \hat{X}{t})) \
&\approx g{\text{forecasting}}(f_{\text{encoding}}(\hat{X}{t-J+1}, \hat{X}{t-J+2}, \ldots, \hat{X}_{t}))
\end{align}
$$
这种结构也类似于 LSTM 未来预测模型,只是输入与输出元素都是 3 D 张量,保留了所有的空间信息,由于网络中堆叠了多个 ConvLSTM 层,它具有强大的表示能力,使其适合于在复杂动态系统中进行预测。
模型评估
Moving-MNIST
实验表明,ConvLSTM 网络在性能上始终优于 FC-LSTM。更深的网络可以产生更好的结果。同时,还尝试了其他的配置,将 2 层,3 层网络的状态到状态和输入到状态的卷积核更改为 1*1 与 9*9。尽管新 2 层网络的参数接近原始网络,但是结果变得更差,因为 1*1 的状态到状态转换很难捕捉到时空运动模式。
新的 3 层网络比新 2 层网络表现更好,因为更高的层可以看到更广泛的输入范围。

雷达回波数据集
可以从以下数据中看到:
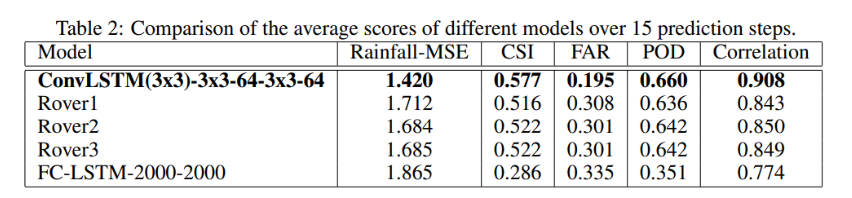
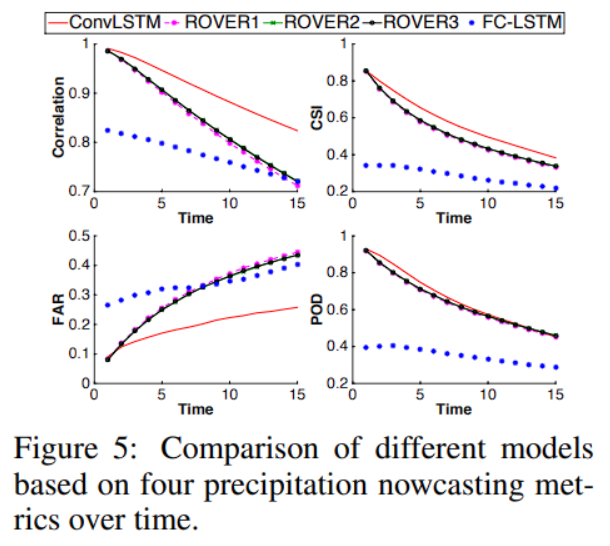
FC-LSTM 网络在此任务上表现不佳。ConvLSTM 可以很好的处理边界条件。
有以下两个原因:
- ConvLSTM 可以很好的处理边界条件。
- ConvLSTM 是为此任务端到端训练的,网络的非线性和卷积结构可以学习数据集中的一些复杂时间模式。