Rewrite the Stars
论文地址:arxiv
摘要
当前对星操作(逐元素乘法)的应用很多,但是没有可以解释其原理。
创新点
本研究揭示星操作将输入映射到高维非线性特征空间的能力(类似于核技巧(kernel tricks))而不需扩展网络。
介绍了 Starnet,在紧凑的网络结构和高效的预算下展示了高性能与低延迟。
正文
介绍
学习范式(learning paradigms)已经发生了改变,从 alexNet 到自注意力机制到星操作(star operation)。星操作:通过元素级乘法融合不同的子空间特征。因为元素级乘法符号类似于星号。
作者构建出了一个用于图像分类的演示块:
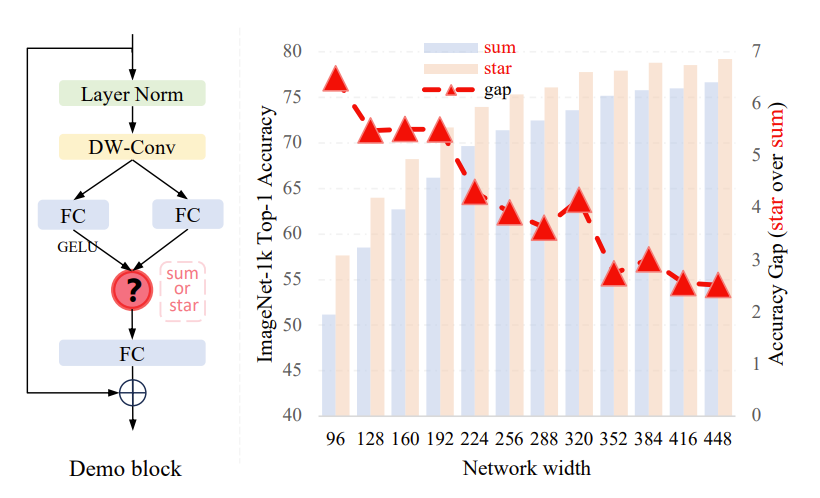
在一层初始块后堆叠多个演示块,构建了 DemoNet 的简单模块,在保持其他因素不变的情况下,可以发现星操作在性能上始终优于求和(可以在右侧的图中看到)。
而当前的研究中基于直觉与假设,没有全面的分析与有力的证据。所以星操作的基础原理没有充分的研究。
而在本论文中,通过明确展示星操作具有输入映射到极高维非线性特征空间的能力,解释了其强大的代表性能力。探讨了星操作的细节,通过重写与重新表述星操作,可以发现这种操作可以生成一个包含大约 $(\frac{d}{\sqrt{2}})^2$ 个线性独立维度的新特征空间。
星操作实现这种非线性高维度的方式与通过增加网络宽度(通道数量)来增加维度的神经网络不同。星操作类似于跨不同通道进行特征对乘的核函数,特别是多项式核函数。当被纳入神经网络并堆叠多层时,每一层都对隐含维度复杂性的指数级增长有所贡献。所以只需要有几层,星操作就可以在紧凑的特征空间内实现近乎无限的维度。
基于以上内容。作者推断星操作可能天生更适合高效,紧凑的网络,而不是传统使用的大型模型。因此设计了 StarNet,其架构如下:
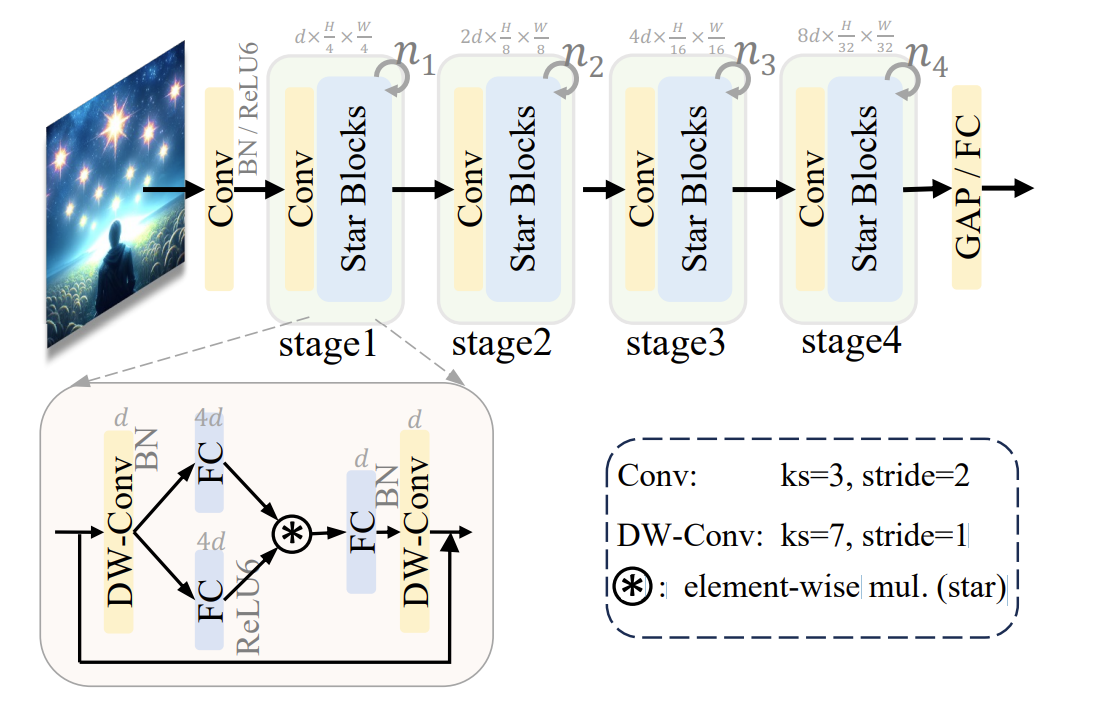
该网络的准确率高,性能也高。
贡献
- 展示了星操作的有效性
- 通过实证结果,理论探索,可视化表示验证了分析
- 提出了概念验证模型 StarNet
- 引导研究人员避免随意的网络设计尝试
相关工作
无论是微小的架构修改,元素级乘法都是至关重要的。它有能力以一种新的方式隐式地将输入特征转换为异常高且非线性的维度,但在低维空间中运行。
在机器学习算法与深度学习网络中,高维和非线性特征的引入至关重要。因为现实世界数据的复杂性与模型要可以表示这种复杂性的能力。在传统网络中,通常用线性投影低维特征到高维空间开始,然后使用激活函数。而本文中使用核技巧(kernel tricks)同时实现高维和非线性,比如:$k(x_1,x_2)=(\gamma x_1 * x_2+c)^d$ 可以将输入特征 $x_1,x_2$ 投影到 $(n+1)^d$ 的高维非线性特征空间。相反,经典机器学习核方法和神经网络在实现和理解高维和非线性特征这方面有所不同。
在本次论文中,作者展示了星操作可以在低维输入中实现向维和非线性特征空间。以下是星操作与多项式核函数之间的联系:

从上图可以看到:星型网络的决策边界比求和法更有效,而且,与多项式核 SVM 的边界非常接近。
重写星操作
通过重写星操作,来展示其可以实现极高维度的能力。
单层中的星操作
在单层神经网络中,星操作通常写作 $(W^T_1 X + B_1) \cdot (W^T_2 X + B_2)$,这表示通过元素级乘法融合两个线性变换的特征。为了方便,将权重矩阵和偏置合并为一个实体,令 $W=\begin{bmatrix} W\ B \end{bmatrix}$,$X=\begin{bmatrix} X \ 1 \end{bmatrix}$,结果星操作为 $(W^T_1 X) \cdot (W^T_2 X)$ 。为了简化分析,聚集于单输出通道亦称与单元素输入的情况:定义 $w_1,w_2,x$,其中 $d$ 为输入通道数量。这个定义可以很容易地扩展以适应多输出通道 $W_1,W_2$ 和处理多个特征元素。通常使用以下方式重写星操作:
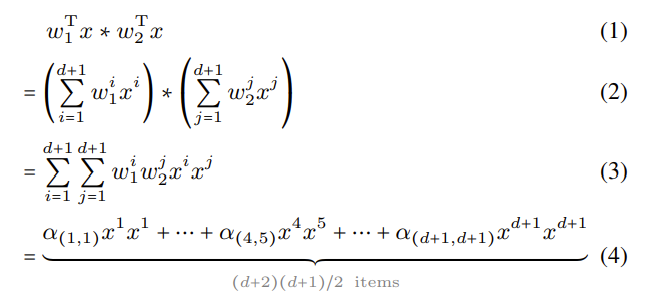
使用 $i,j$ 来索引通道,$\alpha$ 是每个项的系数:
$$
\alpha(i,j) =
\begin{cases}
w^i_1 w^j_2 & \text{if } i = j, \
w^i_1 w^j_2 + w^j_1 w^i_2 & \text{if } i \ne j.
\end{cases}
\ \ \ \ \ \ \ (5)
$$
通过重写公式 1 的星操作,可以将其扩展为 $(d+2)(d+1)/2$ 个不同的项(正如公式 4 所示)。而且,除了 $\alpha (d+1, :) x^{d+1} x$ 之外的所有项都与 $x$ 存在非线性关联,所以它们是独立且隐含的维度。
由上可知:在 d 维空间内使用星操作,可以在 $\frac{(d+2)(d+1)}{2} \approx ( \frac{d}{\sqrt {2}})^2$ 的隐藏维度特征空间内实现表示,显著的放大了特征维度。并且在单层内没有产生任何额外的计算开销(星操作能够在不增加计算开销的情况下,将特征维度从 $d$ 扩展到 $\frac{(d+2)(d+1)}{2}$。
多层扩展
通过堆叠多层,可以递归的方式将隐含维度指数级地增加到接近无限。如果初始网络层的宽度为 $d$,则应用一次的星操作可提到表达式:
$$
\sum_{i=1}^{d+1} \sum_{j=1}^{d+1} w^i_1 w^j_2 x^i x^j
$$
这可以得到一个隐含特征空间的表示。
令 $O_l$ 表示第 $l$ 次星操作的输出,可以得到:
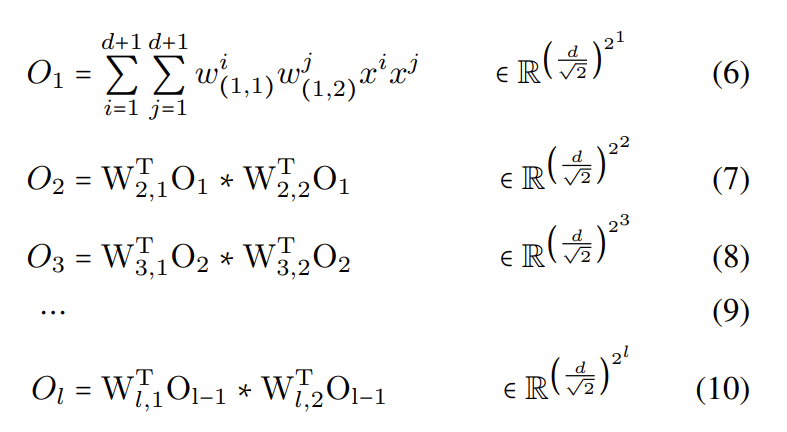
也就是说,通过 $l$ 层,可以隐含的得到一个属于 $\mathbb{R} \left ( \frac{d}{\sqrt{2}} \right)^{2^l}$ 的特征空间。所以,如果给一个宽度为 128 的 10 层各向同性网络,则可以得到隐含特征维度约为 $90^{1024}$。
特殊情况
不是所有的星操作都可以遵循公式 1 中的形式:每个分支都要进行转移。
情况 1:W 1 和/或 W 2 的非线性特性
通过引入激活函数将亦称函数 W 1 和/或 W 2 实现为非线性。然后一个关键方面是它们保持通道通信,如公式 2 所示。这种方式不会影响隐含维度的数量。
情况 2:$W^T_1 X \cdot X$
当移除变换 W 2 时,隐含维度的数量从大约 $\frac{d^2}{2}$ 减少到 $2d$
情况 3:$X*X$
星操作将特征空间 ${x_1, x_2, \ldots, x_d}$ 转换到${x_1 x_1, x_2 x_2, \ldots, x_d x_d}$
星操作及其特殊情况通常与空间交互集成,通常通过池化或卷积实现。也存在情况 1,2,3 同时出现的情况。
验证星操作的有效性
构建了 DemoNet,其架构在上文中有写,星操作与求和操作的对比如下:
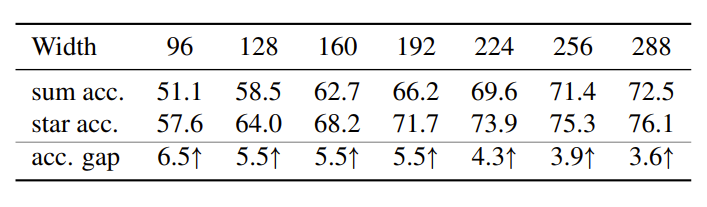
深度为 12,以 32 为单位逐步增加宽度
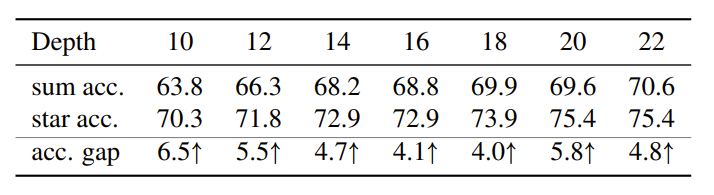
将宽度设置为 192,以 2 为单位逐步增加深度。
决策边界比较
可视化图可在上文找到。该数据集由两组月亮形状的 2 D 点组成。将模型配置为宽度为 100,深度为 4。
显然,星操作划定的决策边界比求和操作更精确和有效。决策边界差异并非源于非线性,因为两种操作在各自的构建块中都包含激活函数。主要区别在于星操作能够达到极高的维度。星操作类似于核函数,特别是多项式核函数。
无激活函数的网络扩展
将 DemoNet 中所有的激活函数移除后,创建出了一个无激活函数的网络,以下是移除前后准确率的对比:
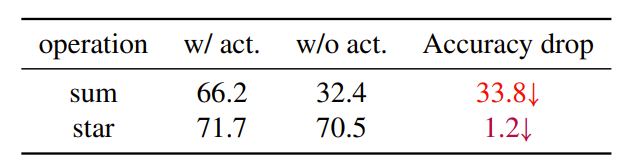
星操作在去除激活函数后仅受到轻微影响。这表明星操作在没有激活函数的情况下仍能保持高效,验证了理论分析并为未来研究提供了方向。
开放讨论
激活函数真的不可或缺吗
星操作引入了隐含的高维度和非线性,这可能使得去除激活层成为可能。
星操作与自注意力(self-attention)和矩阵乘法(matrix multiplication)之间有什么关系
自注意力机制通过矩阵乘法实现全局交互,但这会改变输入的形状,需要额外的调整操作。星操作也具有非线性和高维性,但避免了这种复杂性。本文研究了这两者之间的关系,提供了新的见解。
如何优化隐含高维空间中的系数分布?
传统神经网络可以为每个通道学习不同的权重系数,但星操作中的系数是固定的。这限制了性能的提升。文章提到跳跃连接和密集连接可能有助于解决这一问题,并且采用指数函数可能提供映射到隐含无限维度的途径。
StarNet
StarNet 使用了星操作,用于验证星操作的有效性。StarNet 具有极简的设计,并显著减少了人为干预。
为了避免复杂的设计(重新参数化,SE 块等)影响星操作的有效性,因此没有使用这些人为干预的设计。
架构
StarNet 的架构分为四个阶段,利用卷积层进行下采样,并使用修改后的 demo 块进行特征提取。为了提高效率,批归一化被用来替代层归一化,并放置在深度卷积之后。受 MobileNeXt 的启发,深度卷积被加入到每个块的末尾。通道扩展因子固定为 4,每个阶段的网络宽度加倍。在 demo 块中,GELU 激活函数被 ReLU 6 取代,遵循 MobileNetv 2 的设计。
星操作块的结构如下:
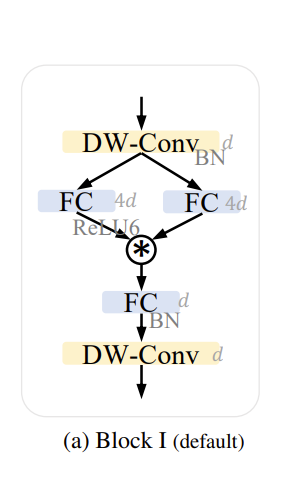
StarNet 的实验
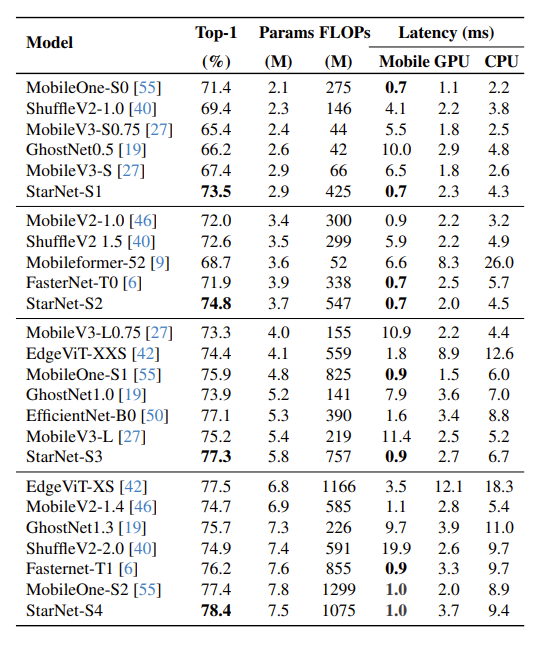
ImageNet-1 k 上高效模型的比较
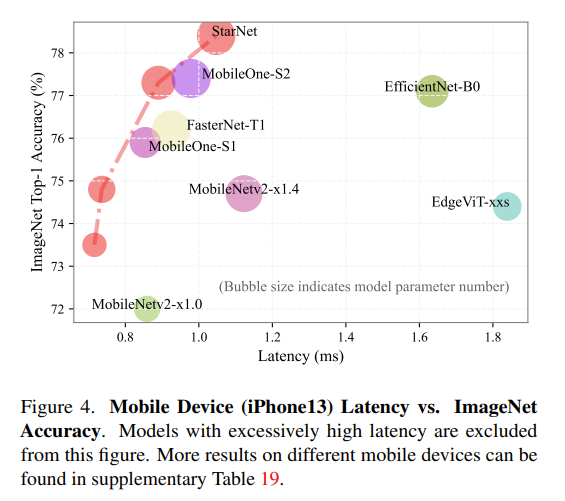
移动设备(iPhone 13)延迟与 ImageNet 准确率对比。
进一步提升性能
可以通过超参数优化,用更多训练增强技术(更多的训练周期或蒸馏)。不过,作者提出,虽然可以通过超参数优化和训练增强技术进一步提升 StarNet 的性能,但他们的主要目标并不是获得高性能模型,而是突出星操作的核心贡献。
消融实验
替换星操作
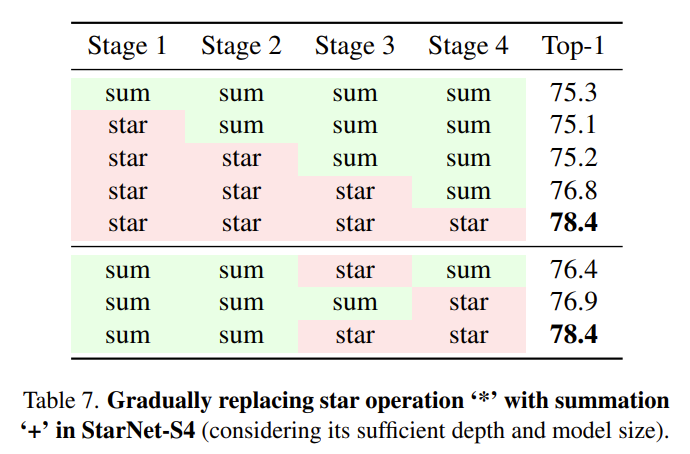
星操作被认为是模型高性能的关键。当用求和操作替换星操作时,模型性能显著下降,尤其是在模型的最后两个阶段。这表明星操作在这些阶段的贡献更大。
星操作的延迟影响
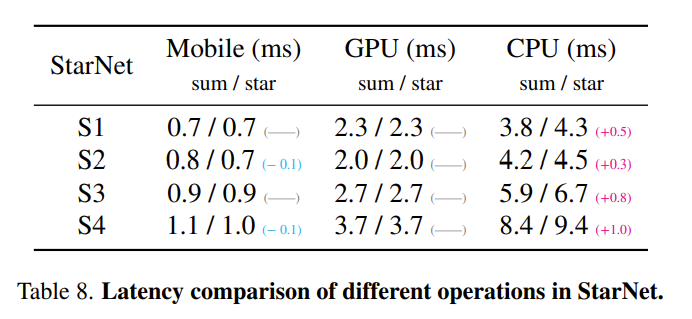
尽管理论上乘法操作比求和操作复杂,但实际测试显示,在 GPU 和 iPhone 上,两者的延迟差异不大,而在 CPU 上,求和操作稍微高效一些。
激活函数位置的研究
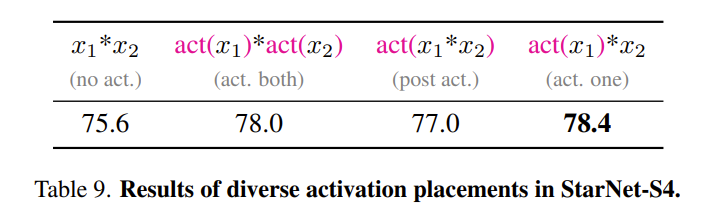
实现激活函数的四种方法:1)不使用激活函数,2)激活两个分支,3)在星操作后激活,4)激活单个分支(默认)。
发现激活单个分支效果最好,而完全移除激活函数影响不大,这表明无激活网络有潜力。
这里使用的激活函数是 ReLU6, x 1 和 x 2 用于表示两个分支的输出
带星操作的块设计研究
将星操作更换为 $(W^T_2 , \text{act}(W^T_1 X)) \cdot X$, $W_1$ 用于扩展宽度,$W_2$ 用于恢复到 d,通过这样做,性能下降。尽管更好的设计可以减小这一性能的差距,但是其差异可以表明初始实现利用星操作能力的有效性,强调了星操作中转换两个分支的关键重要性。
在论文的补充材料中,作者提到:不同块的效果更多地归因于星操作本身,而不是块的具体设计。因此,我们将默认星操作块作为我们 StarNet 的基础块。