决策树与决策森林
决策树
笔记来源:# 机器学习算法–决策树的超生动简单演示
决策树是一个递归分割的二叉树,直接得到纯净的叶结点(数据只包含一种类型的类别,在以下展示的决策树中,一个叶结点中的类型要么是红色,要么是绿色)。决策树是一个贪心算法,无法保证得到的是一个最优的分割集,但是它的训练速度很快,同时效果也很好。
以下是一个决策树。
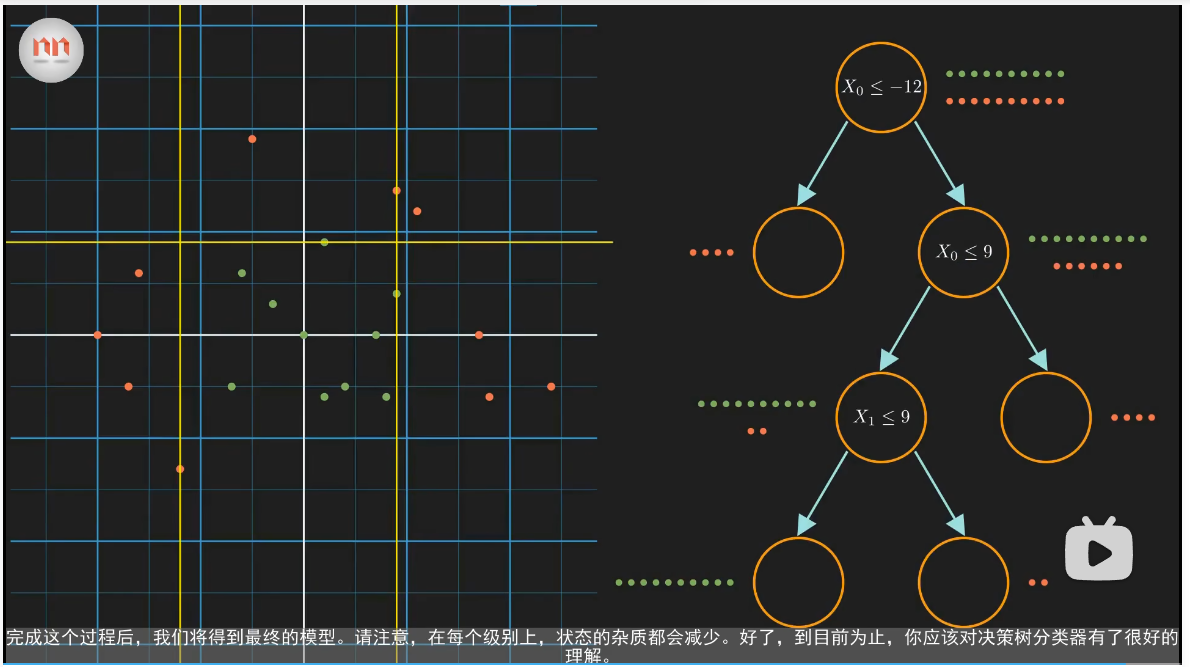
使用决策树分类:设一个新的点为 (15,7),则经过决策树以后,该结点会到一个结点,而该结点中的所有的数据都是红色的,因此该点为红色。
决策树的本质可以看成是一大堆的 if-else 语句。
模型决定最佳的分割:
以根结点为例,该决策树可以选择 y <= 4 与 x <= -12。而对于计算机来说,做一个决策一定要通过一个值来确定,所以这里可以定义: 熵 与 信息增益。
熵是一个状态所包含的信息量的度量,如果熵很高,则不能确定随机选出的点是什么。熵的公式如下:$Entropy = \sum - p_{i}*log_{2}(p_{i})$。 $p_{i}$ 表示第 i 类出现的概率,在本次示例中,如果红色与绿色出现的概率相同,则红与绿的 $p$ 均为 0.5。将该公式代入根结点,则根结点的概率为 1,而纯结点的熵为 0。
信息增益的公式如下:$IG = E(parent) - \sum w_{i}E(child_{i})$。其中,$E(x)$ 表示 x 的熵;$w_{i}$ 表示子结点中的个数比父结点中的个数。
使用该公式可知:x <= -12 的信息增益为 0.24,而 y <= 4 的信息增益为 0.034。因此我们选择 x <= 12 这种分割方式。
模型在实际的运行过程中,会比较每一种分割方式,并选择信息增益最大的分割方式。
缺点:对训练的数据很敏感。
随机森林
笔记来源:# 最生动理解机器学习算法–随机森林
数据集(6 个样本,5 个特征,而目标变量 y 只有 0 与 1 ,是二分类问题):
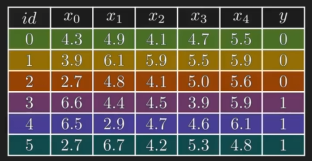
其决策树如下:
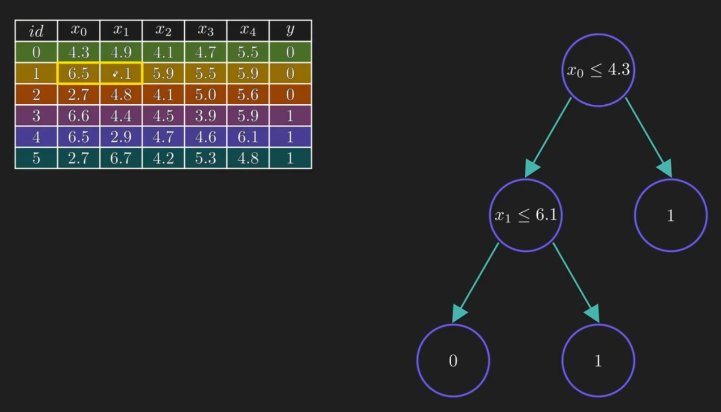
如果修改了 id 为 1 样本中的 x0 与 x1 中的值,则其决策树会完全不同:
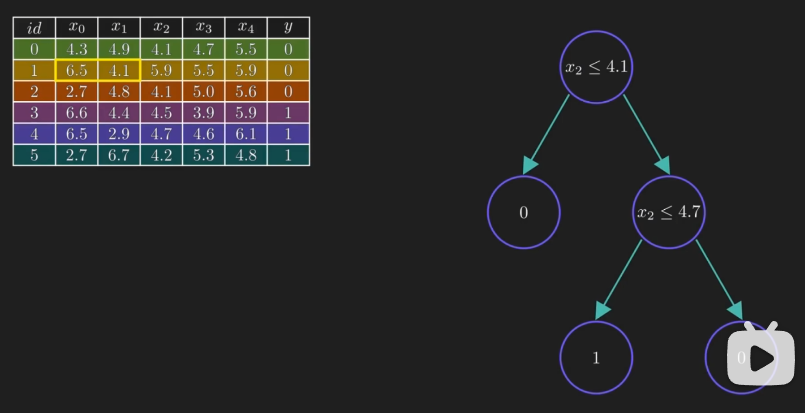
由此可以得知:决策树对训练数据非常的敏感,容易产生高方差。因此,这样的模型在泛化上可能就会有问题。
随机森林是一群随机生成的决策树,对训练数据的敏感度要小得多。由于用了很多树,因此叫其森林。
随机森林的构建:从原始数据中随机挑选行,来构成新的数据集,每个新的数据集的行数与原始数据集是一样的。抽取时,使用 有放回的随机抽样。这样创建数据的过程叫做:自举(bootstrapping)。

现在对每个自举得到的数据集分别训练一个决策树。并且,在训练决策树时,不会使用所有的特征,而是为每棵树随机选取一部分特征,然后使用这些特征来训练。
可以得出以下的随机森林:

现在有一个新的结点:[2.8, 6.2, 4.3, 5.3, 5.5],然后使用每个决策树对这个结点进行分类,得到:[1, 0, 1, 1]。采用多数投票的原则,则可以得到:1 号结点提到了最多的投票,所以,随机森林的预测结点就是 1。可以将以上的过程称为:聚合,从多个模型中整合结点。
在随机森林中,先自举,然后进行聚合,可以使用 bagging = Bootstrap + Aggregating 来描述该过程。
随机森林的随机在于:随机使用数据样子自举,随机选择特征。自举可以确保每棵树使用的数据都不同,这样可以在某种程序上降低模型对原始训练数据的敏感度;随机选择特征则有助于降低树与树之间的相关性,此外,还可以将单一的树给出的不好的结果,通过另一棵树的不好的结果相互抵消。
特征子集的理想大小为:总特征数的对数或平方根。
如果要使用随机森林解决回归问题,则只需要在聚合结果时,取平均值即可。