Wavelet-Driven Spatiotemporal Predictive Learning-- Bridging Frequency and Time Variations
论文地址:aaai
摘要
时空预测是指:使模型通过以无监督的方式从过去的帧预测未来的帧。实现时空预测通常使用循环单元来捕捉长期依赖关系,但是这些单元往往有很高的计算成本,并且在真实场景中性能有限。
而该论文通过基于小波的时空(WaST)框架,该框架通过 3 D 离散小波变换在图像和特征层面提取并自适应地控制低频和高频分量,以实现更快的处理,同时保持高质量的预测。
提出了两点设计:
- 时频感知转换器(Time-Frequency Aware Translator),它被独特地设计用于通过分别建模空间频率和时间变化来高效地学习短程和长程时空信息。
- 小波域高频焦点损失(wavelet-domain High-Frequency Focal Loss),有效地监督高频变化。
正文
时空预测学习
通常有两种方法来建模:基于循环与无循环框架。
以上两种方式如下图所示:
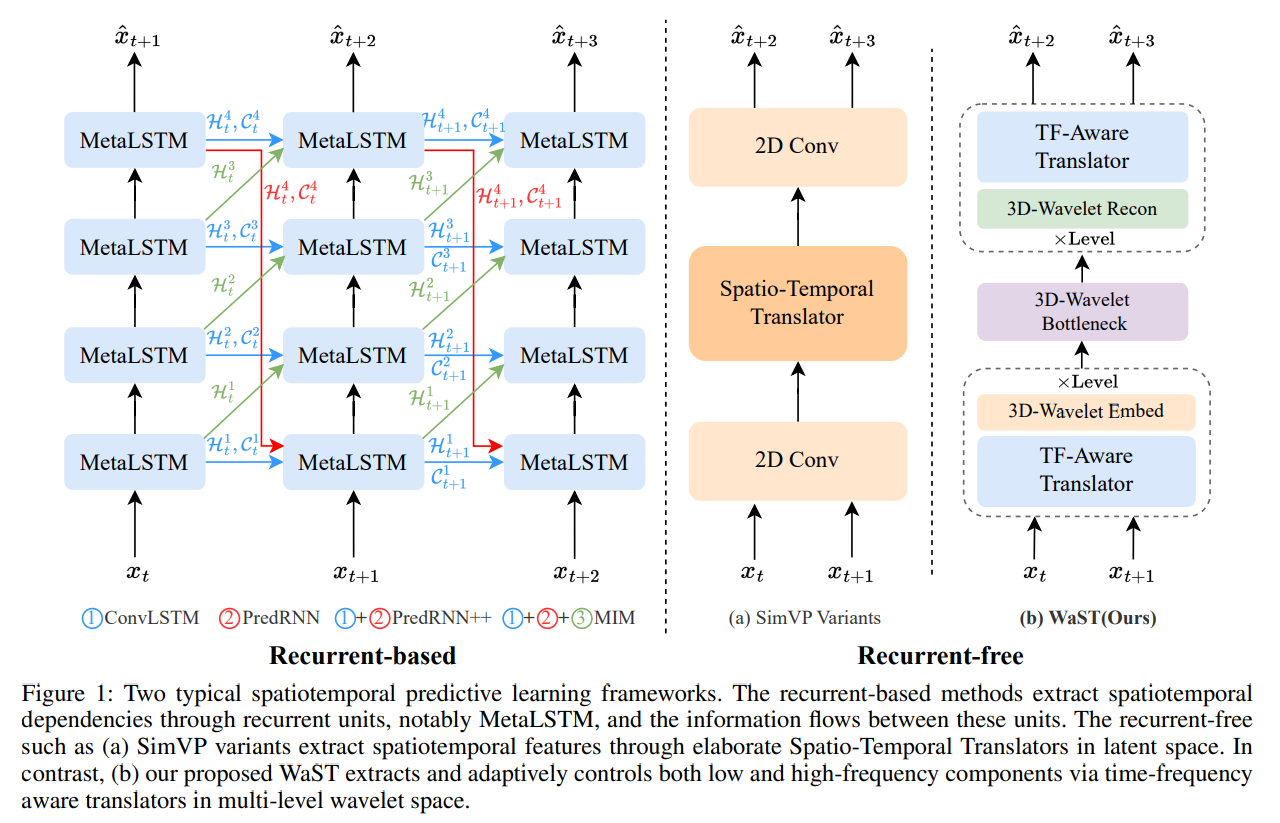
基于循环
左图为基于循环的模型的一般框架,其主要由两个部分组成:
- 将各种 LSTM 变体,称为 MetaLSTM
- 不同循环单元之间的信息流模式
虽然这种框架在长期预测方面有优势,但是其计算量很大,限制了其发展。
无循环
最近,具有并行化执行的无循环方法被提出并用于时空学习。a 图为代码 SimVP 各种变体的无循环框架,它也是由两个部分组成:
- 空间 2 D 编码器-解码器
- 潜在特征时空转换器
这个框架的计算效率更高,但是由于单尺度构,2 D 操作与不稳定的时空转换器,这个方法也有着性能的差距
作者的网络特征
作者提出了一种新颖的基于小波的时空 (WaST) 预测方案来解决现有的性能差距。他们的解决方案依赖于多级 3 D 离散小波变换 (3 D-DWT),它将数据分解为低频和高频小波子带。
- 作者引入了 3 D 小波嵌入和重建模块,分别用于嵌入小波先验和执行细节导向的重建。
- 为了学习复杂的频率特征和时间动态,作者提出了一个时频感知转换器 (TF-Aware Translator),通过频率混合器和时间混合器来提取和自适应控制多级小波空间中的低频和高频分量。
- 作者引入了一个小波域高频焦点损失 (HFFL),它还能捕捉小波域中连续和静态帧之间的快速变化。作者认为传统的均方误差损失难以关注细节特征。
创新点
- 提出了一种开创性的基于小波的时空(WaST)预测茄,通过高频分量提高计算效率,同时确保高质量预测
- 设计了一个时频感知转换器 (TF-Aware Translator),通过分别建模空间频率和时间变化,有效地学习现实世界的时空依赖关系。
- 我们提出了一个小波域高频焦点损失 (HFFL) 来监督高频变化。
创作动机
虽然当前的无循环模型(TAT,SimVP,TAU,DMVFN)等在多方面有了很大的进展,但是大多数工作没能考虑真实世界动态场景中的依赖性,从而导致预测细节的缺失。
所以作者使用 3 D 小波框架和时频感知转换器来解决这些问题。
此外,虽然小波变换已经有了很多的使用,但是作者认为其还有很大潜力,所以提出了一种新颖的基于 3 D 小波的方案,以实现更好的时空学习。
问题定义
时空预测是指在给定的过去帧 $X_{in}$ 进行建模,来预测未来帧 $X_{out}$,可以将时空序列表示为四维的张量,即:$X_{in}^{t:T} \in R^{CTHW}$ 与 $X_{out}^{T+1:T+T’} \in R^{CT’HW}$,其中,$C,T,H,W$ 分别为通道,时间,高度,宽度。通过具有可学习参数 $\theta$ 的模型通过探索时空依赖关系来学习映射 $F_{\theta}: X_{in}^{t: T} -> X_{out}^{T + 1:T + T’}$。作者使用随机梯度下降法来学习映射 $F_{\theta}$ 并找到一组参数 $\theta^{}$,并以最小化预测未来帧与真实帧之间的差异,最优的参数 $\theta^{}$ 为:
$$
\theta^* = \arg \min_{\theta} L(F_{\theta}(X^{t:T}{\text{in}}), X^{T+1:T+T’}{\text{out}})
$$
其中,$L$ 表示损失函数。
在配方中,将视频佟大为一个典型的实验领域,观察到的数据是具有三个通道的 RGB 图像,在其他领域中,观察到的数据是多通道张量。
小波变换的选择
小波变换是一个传统技术,可以从原始数据中分离出低频与高频细节。一般来说,小波变换处理输入信号涉及两种操作:离散小波变换(DWT)与逆离散小波变换(IDWT)。由于其简单性,作者在本文中使用了 Haar 小波,利用 $F_L=\frac{1}{\sqrt{2}}[1 \ 1 \ 1]$ 与 $F_H=\frac{1}{\sqrt{2}}[-1 \ 1 \ 1]$ 作为 3D-DWT 的低能与高通过滤器。使用 $F_L$ 与 $F_H$ 构建八个步幅为 2 的核:$F_{LLL},F_{LLH},F_{LHL},F_{LHH},F_{HLL},F_{HLH},F_{HHL},F_{HHH}$。多级 3D-DWT 进一步以递归的方式细化这些子带分量。为了将小波技术引入时空预测学习,作者提出了一个 3 D 小波框架和小波域高频焦点损失(HFFL)。
网络结构
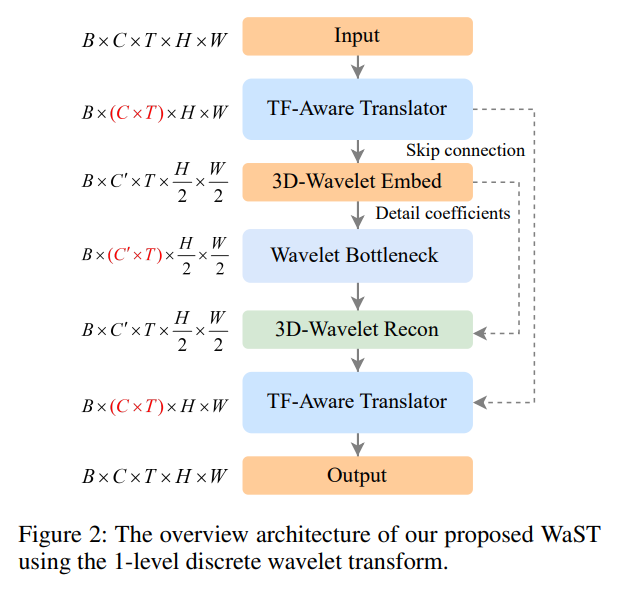
以 1 级离散小波变换为例,以上是其整体架构。
时频感知转换器(TF-Aware Translator)被实现用来学习多级小波空间频率的时间变化。
3 D 小波嵌入和重构模块(3D-Wavelet Embed & Recon)利用小波固有的多尺度架构来嵌入和重构复杂的时空特征。
小波瓶颈块(Wavelet Bottleneck)专注于中间低频表示,同时保留高频细节。
时频感知转换器
时频感知转换器(TF-Aware Translator)通过频率混合器(FM)与时间混合器(TM)分离帧内频率与帧间时间动态的建模。其结构如下所示:
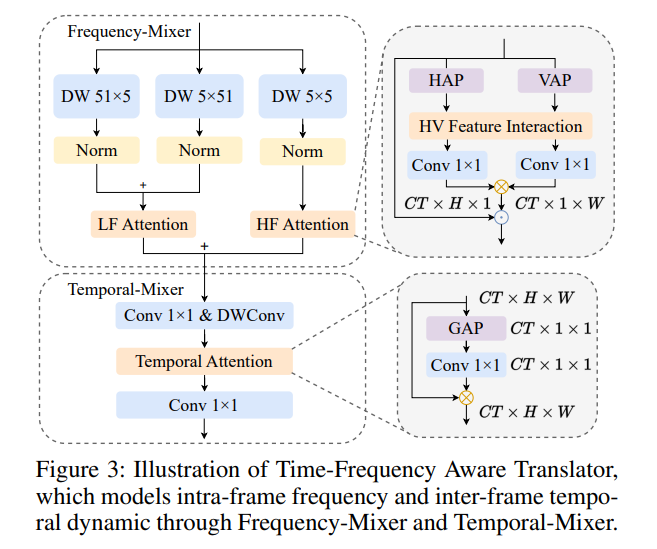
这个模块合并了通道与时间维度。将输入的序列 $X \in R^{BCTHW}$ 重塑为 $B*(C*T)HW$。
转换器的可以表述如下:
$$
X’l = X_l + \text{diag}(\lambda{l,1}, \ldots, \lambda_{l,d}) \times FM(\eta(X_l))
$$
$$
X_{l+1} = X’l + \text{diag}(\lambda’{l,1}, \ldots, \lambda’_{l,d}) \times TM(\eta(X’_l))
$$
其中,$\lambda_{l}$ 与 $\lambda’_{l}$ 是可学习的参数,$\eta$ 为预归一化。
频率混合器
频率混合器由两个关键元素组成:频率特征提取器与频率注意力。
作者使用非对称卷积来拟合超大卷积核(如 51*51)来建模低频特征,并使用并行小卷积核(如 5*5)来建模高频特征。
为增强小波中水平与垂直细节的表示,作者提出了频率注意力机制。
为了自适应地增强不同频率的小波特征(如水平与垂直细节系数),频率注意力被划分为水平与垂直分量,通过挤压-激励范式进行细化,并通过权重共享的 1*1 卷积促进交互,其可以被表示为:
$$
A_H = W_{1 \times 1} * (W^*_{1 \times 1} * HAP(X))
$$
$$
A_V = W_{1 \times 1} * (W^*_{1 \times 1} * VAP(X))
$$
$$
X’ = A_H \otimes A_V \odot X
$$
其中,$$ 为卷积操作。HAP 与 VAP 表示水平与垂直平均池化(AP)。$A_H \in R^{B(CT)H1}$ 与 $A_V \in R^{B(C*T)1W}$ 表示水平与垂直注意力交互的权重共享。$\otimes$ 与 $\odot$ 分别表示 Kronecker 积和 Hadamard 积。
C*T*H*1 与 C*T*1*W 的矩阵经过 Kronecker 积后,其形状为 C*T*H*W。(C,T 维度不会变:两个矩阵在这两个维度下是对齐的,所以相当于元素级乘法)
时间混合器
时间混合器通过结合前馈网络(FFN)和时间注意力来建模长期依赖性。FFN 包含两个 1*1 卷积和一个深度可分离卷积(DWConv)。时间注意力以挤压-激励的方式为帧间动态建模通道与时间维度。其过程可以定义如下:
$$
A_T = W_{1 \times 1} * GAP(X)
$$
$$
X’ = A_T \otimes X
$$
GAP 为全局平均池化。
3 D 小波嵌入和重构
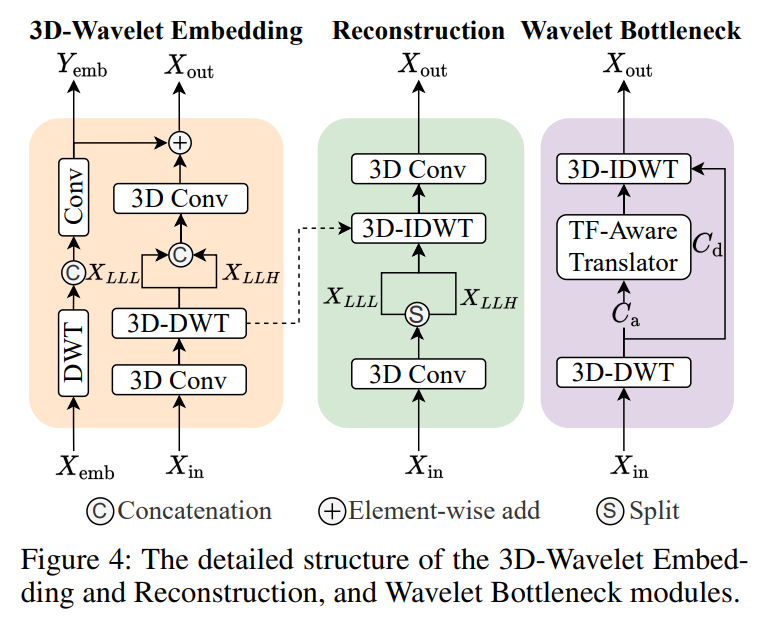
3 D 小波嵌入模块将小波先验集成到特征图中,而重构模块从高频系数恢复细节。小波瓶颈块强调低频表示,同时保留高频细节。
3 D 小波嵌入
利用小波变换的固有属性和可学习的 3 D 卷积来实现更好的下采样。
设计了两个并行分支,一个分支通过 3 D-DWT 和 3 D Conv 将图像特征 X_emb 嵌入到输出特征 X_out 中,另一个分支完成输入特征图 X_in 的空间下采样。在下采样过程中,我们连接 X_LLL 和 X_LLH,将剩余系数 C_detail(例如 X_LHL、X_LHH、X_HLL、X_HLH、X_HHL 和 X_HHH)输入到重构模块以进行细节重构。
3 D 小波重构
在上采样过程中,使用空间低频特征 X_LLL 和 X_LLH,以及来自嵌入模块的细节系数 C_detail,通过 3 D-IDWT 和可学习的 3 D Conv 重构细节。
小波瓶颈
通过转换器和小波变换实现。每个小波瓶颈块首先将特征图 X_in 分解为近似系数 C_a 和细节系数 C_d。然后将 C_a 作为输入传递给转换器进行更深层次的处理。处理后的 C_a 和原始细节子带 C_d 通过 3 D-IDWT 变换回原始空间,这允许聚焦低频特征同时保留高频细节。
小波域高频焦点损失
传统的均方误差 (MSE) 损失对每个像素同等对待,这使得它更强调低频监督。为了弥补 MSE 中高频监督的不足,作者提出了小波域高频焦点损失 (HFFL) 来监督高频变化。
焦点频率损失 (FFL) 旨在减少真实图像和生成图像之间的频率距离。它可以定义为:
$$
L_{FFL} = \frac{1}{HW} \sum_{u=0}^{W-1} \sum_{v=0}^{H-1} w(u, v) \left| F_r(u, v) - F_f(u, v) \right|^2
$$
$$
\text{其中} \quad w(u, v) = \left| F_r(u, v) - F_f(u, v) \right|^\alpha
$$
权重矩阵 w (u, v) 由频率特定的训练损失引导。
然而,由于大的动态频率范围,这种方法不能充分反映高频差异。因此,我们通过对高频带引入对数绝对值|log (w (u, v))|来细化 FFL 的权重矩阵,同时通过预定义阈值τ将低频权重设置为零。我们进一步以多尺度方式细化频域损失,采用小波变换将信号分解为多级子带,小波域高频焦点损失可以定义为:
$$
L_{HFFL} = \frac{1}{H_k W_k} \sum_{u=0}^{H_k-1} \sum_{v=0}^{W_k-1} w(u, v) \left| F_r(u, v) - F_f(u, v) \right|^2
$$
$$
\text{其中} \quad w(u, v) = \left| \log \left( \left| F_r(u, v) - F_f(u, v) \right| \right) \right|^\alpha
$$
其中 k 表示 k 级小波分解。模型通过结合每帧的空间域和小波域损失的目标函数进行端到端训练:
$$
L = L_{MSE}+\lambda L_{HFFL}
$$
解释
计算机视觉中的小波变换
小波变换是时频分析的重要工具,增强了基于 CNN 的视觉任务的性能。
小波变换是一种将信号分解为不同尺度和位置的基本波形(称为小波)的线性变换。这些小波是由一个称为母小波的基本函数通过平移和缩放得到的。
其特点:(局部,多尺度)
- 多分辨率分析:小波变换可以在不同的尺度上分析信号,提供多分辨率的时频表示。
- 局部化:小波在时间和频率域都具有良好的局部化特性,可以捕捉信号的局部特征。
- 灵活性:通过选择不同的母小波函数,可以适应不同类型的信号分析需求。
与傅里叶的对比:
- 信号类型
- 对于平稳信号,傅里叶变换通常足够。
- 对于非平稳信号或需要时频联合分析的场景,小波变换更适合。
- 分辨率
- 傅里叶适合固定的分辨率
- 小波适合多分辨率,低频时有好的频率分辨率,高频时有好的时间分辨率
- 应用
- 傅里叶适合周期性模式的特征提取
- 小波变换在数据分析,图像处理任务中更加灵活
其种类有以下两类:
- 连续小波变换(CWT):适用于连续信号的分析。
- 离散小波变换(DWT):适用于离散信号,计算效率更高。
应用:可以作为神经网络的预处理步骤,提供多尺度特征。
小波变换的强大之处在于它能够提供信号的时频局部化表示,这使得它在处理非平稳信号和捕捉信号局部特征方面具有显著优势。在计算机视觉和人工智能领域,小波变换为复杂的时空数据分析提供了有力的工具,特别是在需要同时考虑时间和频率信息的应用场景中。