深度学习的学习笔记04

发表于 更新于 分类于 ，

本次的主题是ResNet+ResNeXt

视频来源：bilibili，bilibili

论文阅读与视频学习

Deep Residual Learning for Image Recognition，CVPR2016

神经网络的深度非常重要，很多模型都已经达到了很深的深度。但是过深的神经网络会带来

  1. 梯度消失，梯度爆炸的问题。可以通过归一化神经化与中间归一化层来解决。
  2. 退化问题：随着网络深度的增加，准确度变得饱和，然后迅速退化。这种过拟合不是由过拟合引起的，添加更多的层会导致更高的训练误差。

为了解决退化的问题，引入了残差学习框架。

残差神经网络的特点：

  1. 即使当网络很深时，也可以很容易的被优化。（普通的网络会在深度增加时，训练误差也会增加）
  2. 残差神经网络可以很轻松的从深度增加中得到准确率，从而效果比浅层的更好。

准备工作：

  1. 残差表示：VLAD 是一种由残差向量相对于字典进行编码的表示，而 Fisher Vector 可以表述为 VLAD 的概率版本。已经被证明比编码原始向量更有效。此外，使用预处理也可以更好的简化优化。
  2. Shortcut 连接：一个 inception 层由一个 shortcut 与一些更深的网络层构成。在训练时，即使当网络层的输出接近于 0，下一个 inception 层依然可以通过 shortcut 的值进行学习。虽然这种方式可以训练极深的网络，但是准确率不会无限提高，比如超过 100 层后。

深度残差学习

残差学习

假设 $H(x)$ 为希望通过几层神经网络来拟合的函数，x 为输入。同时，多个非线性层可以渐近地逼近复杂的函数。

如果 $H(x)$ 与输入的 $x$ 的维度相同，那么可以让神经网络层逼近残差函数 $H(x)-x$。令 $F(x)=H(x)-x$，即：让神经网络逼近 $F(x)$。此时，$H(x)$ 可以表示为 $F(x)+x$，即:经过神经网络的结果加上输入的值。虽然这两种形式在理论上都可以逼近所需的函数，但是学习的难易程度可能不同。

退化问题指的是随着网络层数增加，模型的训练误差不降反升，而理论上如果新增的层可以构造成恒等映射，更深的模型的训练误差不应大于较浅模型的训练误差，但求解器在通过多个非线性层逼近恒等映射时可能会遇到困难，因此通过残差学习的重新表述可以有助于处理这种问题。

Shortcut 的种类

  1. 使用零填充捷径来增加维度
  2. 使用投影捷径来增加维度
  3. 所有的捷径都是投影捷径

区别：

  • 效果：3 > 2 > 1
  • 内存使用：3 > 2 > 1

使用捷径有助于训练，３种类型的捷径的区别不大，并且都会比不使用捷径的效果好。

恒等捷径是指直接将输入传递到输出，而不进行任何变换或参数调整。在上面的三种捷径的种类中，配置 1 和配置 2 中的一部分，用于那些不需要增加维度的连接。

网络结构

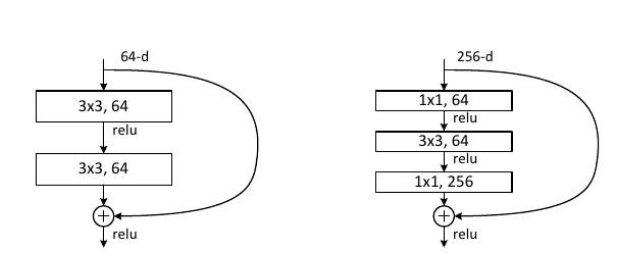
左侧的为 18 层，34 层，50 层的网络使用的结构，为了减少参数，设计了右侧的结构。右侧的结构通过先降维后升维的方式，使得神经网络的参数减少，最终使得神经网络的训练时间控制在可以接受的时间范围内。

实验对比

通过 vgg19，普通卷积网络, 残差神经网络 的对比，可以得出：

  1. 对于普通网络，越深的网络，训练误差越大
  2. 对于残差网络，越深的网络，精度越高
  3. 残差网络可以在参数量很少的情况下精度胜过 vgg19

以上总结：残差网络打赢了当时大部分网络，是更好的一种网络模型

后续使用了 1202 层的残差神经网络，来探究极限，发现出现了可能是过拟合的情况。’

ResNet视频学习

ResNet网络简介

普通网络中存在的问题

  • 梯度消失或梯度爆炸
  • 退化问题（degradation problem）

解决梯度问题的一般方式：

  • 对数据进行标准化处理
  • 权重初始化
  • batch normalization 处理

解决退化问题：

  • 残差结构

ResNet 的特点

  • 超深的网络结构（超 1000 层）
  • 提出 residual 模块
  • 使用 Batch Normalization 加速训练

BasicBlock

主分支的输出特征矩阵的高宽，通道要与输入特征矩阵的高宽，通道都保持一致。这两个要相加。

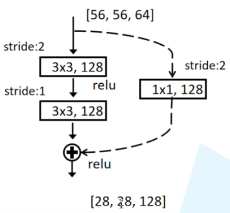
对于每个模块的第一层网络，由于该网络要将输入的尺寸改变（通过将 stride 设置为2 来使得高与宽变为原来的一半），所以 shortcut 处要对输入的数据也做相应的变换，这样才可以与主分支相加。

Bottleneck Block

  • 最上面的卷积层用于降维
  • 最下面的卷积层用于升维

这种结构的特点是，初始的结构，参数降低了约一半。

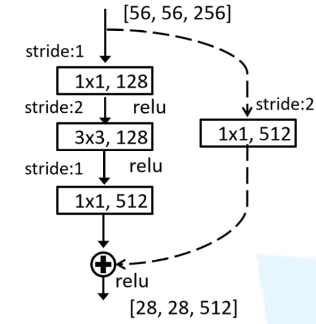
  • 原理与上文一致

Batch Normalization

  • 目的是使一批 batch 的 feature map 满足均值为 0，方差为 1 的分布规律。原因：虽然图像经过了预处理以后，可以满足某一个分布规律，但是经过卷积层以后，得出的 feature map 则不一定满足这个分布规律。

可以加速网络的收敛并且提升准确率。

使用 BN 时需要注意的问题

  1. 训练时要将 training 参数设置为 True，在验证时将 training 参数设置为 False。在 pytorch 中可以通过创建模型的 model.train() 和 model.eval() 方法控制。
  2. batch size 尽可能设置大点，设置小后表现可能很糟糕，设置的越大求的均值和方差越接近整个训练集的均值与方差
  3. 建议将 bn 层放在卷积层和激活层之间，肯卷积层不要使用偏置 bias（即使使用了，经过 bn 层以后也不会起效果）。

迁移学习简介

优点：

  • 可以快速训练出一个理想的结果
  • 当数据集较小时也可以训练出理想的效果
  • 使用别人预训练的模型参数时，也要注意别人的预处理的方式

常见的迁移学习的方式：

  1. 载入权重后训练所有参数
  2. 载入权重后只训练最后几层参数
  3. 载入权重后在原网络基础上再添加一层全连接层

Aggregated Residual Transformations for Deep Neural Networks， CVPR 2017

网络准确度的提升可以像 VGG 一样，通过堆叠相同的模块来实现，也可以像 Inception 一样，通过拆分，转换，合并的方式来实现。这个网络通过结合这两种方法来实现了更进一步的准确度的提升。这种方式实现了在保持（或降低）复杂度的同时提高准确度。

ResNeXt 的核心是使用分组卷积来构建一个网络层。通过使用分组卷积来结合 Inception 的拆分，转换，合并的网络构建思想，然后再通过堆叠相同的模块来结合 VGG 的思想。

论文中定义了一个名词 cardinality，描述分组卷积中，组数的数量。实验中证明了，增加 cardinality 会比增加网络的深度与广度对准确度更有效果，尤其是出现退化问题的时候。而 cardinality 是一个具体的，可以测量的量。

改进过程：

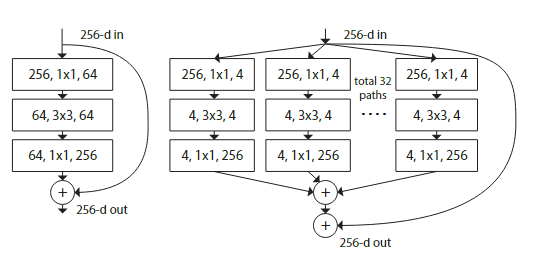
左侧是 ResNet 的模块，而右侧是最初的 ResNeXt 的模块。这两者有着几乎相同的计算量。

而为了简化左侧模块的计算量，可以在数学上做一个等价变形：

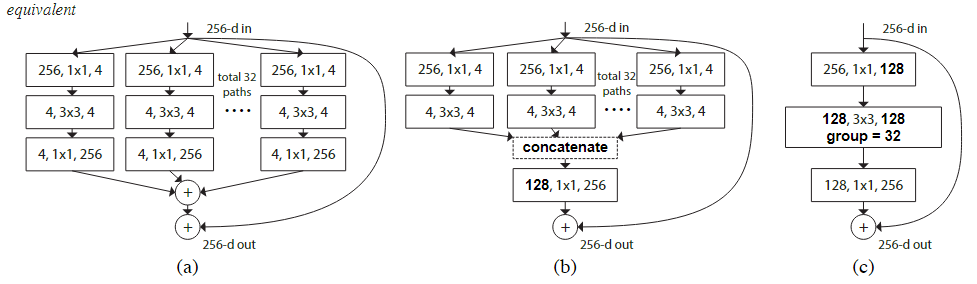
  • 32 组的 4, 1*1, 256 的卷积后连接可以转换为先对中间层的结果进行拼接后再使用一个 128, 1*1, 256 的卷积。
  • 32 组的 256, 1*1, 4 可以等价成一个 256, 1*1, 128，而 32 组的 4, 3*3, 4 可以等价成一个 128, 3*3, 128, group=32

这种等价变换的关键在于分组卷积的特性，它允许将一个大的卷积操作分解成多个小的、独立的卷积操作，每个操作只在自己的通道组内进行。这样，可以在不改变模型计算复杂度的情况下，增加模型的 cardinality，从而提高模型的表示能力。这种特点只有当网络块具有足够的深度时才可以体现出来：此时，分组卷积才可以形成多个独立的，并行的变换路径，从而增加模型的复杂性与多样性。

分组大小选择 32 的原因：

  • 模型有足够的复杂性来捕捉数据中的模式
  • 当大于 32 时，对于模型的准确度提升不大，但是训练花费的时间却大幅增加

课后作业

代码作业

以下分别是LeNet网络与ResNet网络的模型

LeNet网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 使用类似于LeNet 的网络来分类猫与狗
# 输入： 3 * 256 * 256
class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        # 3 * 256 * 256
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=24, kernel_size=3, bias=False)
        # 16 * 254 * 254
        self.batch1 = nn.BatchNorm2d(24)
        self.pool1 = nn.MaxPool2d(kernel_size=2)
        # 16 * 127 * 127

        self.conv2 = nn.Conv2d(in_channels=24, out_channels=32, kernel_size=3, bias=False)
        # 24 * 125 * 125
        self.batch2 = nn.BatchNorm2d(32)
        self.pool2 = nn.MaxPool2d(kernel_size=2)
        # 24 * 62 * 62
        self.conv3 = nn.Conv2d(in_channels=32, out_channels=32, kernel_size=3, bias=False)
        # 24 * 60 * 60
        self.batch3 = nn.BatchNorm2d(32)
        self.pool3 = nn.MaxPool2d(kernel_size=2)
        # 24 * 30 * 30
        self.fc1 = nn.Linear(32 * 30 * 30, 72)
        self.fc2 = nn.Linear(72, 36)
        self.fc3 = nn.Linear(36, 2)


    def forward(self, x):

        x = self.conv1(x)
        x = self.batch1(x)
        x = F.relu(x)
        x = self.pool1(x)

        x = self.conv2(x)
        x = self.batch2(x)
        x = F.relu(x)
        x = self.pool2(x)

        x = self.conv3(x)
        x = self.batch3(x)
        x = F.relu(x)
        x = self.pool3(x)

        x = x.view(x.size(0), -1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.softmax(self.fc3(x), dim=1)
        return x

ResNet网络

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class BasicNetBlock(nn.Module):
    expansion = 4

    def __init__(self, in_channel, out_channel, stride):
        super(BasicNetBlock, self).__init__()

        self.stride = stride
        self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=out_channel, kernel_size=1, bias=False)
        self.bn1 = nn.BatchNorm2d(out_channel)
        self.conv2 = nn.Conv2d(in_channels=out_channel, out_channels=out_channel, kernel_size=3, bias=False,stride=stride, padding=1)
        self.bn2 = nn.BatchNorm2d(out_channel)
        self.conv3 = nn.Conv2d(in_channels=out_channel, out_channels=out_channel * self.expansion, bias=False, kernel_size=1)
        self.bn3 = nn.BatchNorm2d(out_channel * self.expansion)

        if stride != 1 or in_channel != out_channel * self.expansion:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_channels=in_channel, out_channels=out_channel * self.expansion, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(out_channel * self.expansion)
            )
        else:
            self.shortcut = nn.Identity()


    def forward(self, x):
        out = self.conv1(x)
        out = self.bn1(out)
        out = F.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = F.relu(out)

        out = self.conv3(out)
        out = self.bn3(out)

        out += self.shortcut(x)

        out = F.relu(out)
        return out

# 输入大小：3*228*228
class ResNet(nn.Module):
    def __init__(self):
        super(ResNet, self).__init__()
        self.in_channel=16
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, bias=False)
        self.bn1 = nn.BatchNorm2d(16)

        self.layer1 = self._make_layer(BasicNetBlock, 16, 3, 1)
        self.layer2 = self._make_layer(BasicNetBlock, 32, 3, 2)
        self.layer3 = self._make_layer(BasicNetBlock, 32, 3, 2)
        self.fc1 = nn.Linear(in_features=32 * BasicNetBlock.expansion *14 *14, out_features=2)

    def forward(self, x):
        # 3*228*228
        x = F.relu(self.bn1(self.conv1(x)))
        # 16*226*226
        x = self.layer1(x)
        # 4*16*226*226
        x = self.layer2(x)
        # 4*32*113*113
        x = self.layer3(x)
        # 4*32*56*56
        x = F.max_pool2d(x, 4)
        # 4*32*14*14
        x = x.view(x.size(0), -1)
        x = self.fc1(x)
        return x

    def _make_layer(self, block, out_channel, blockNumber, stride):
        layers = []
        layers.append(block(self.in_channel, out_channel, stride))
        self.in_channel = out_channel * block.expansion
        for stride in range(blockNumber - 1):
            layers.append(block(self.in_channel, out_channel, 1))

        return nn.Sequential(*layers)

电脑的显存就只有6g，没法搭建太大的网络。经过比赛方给出的训练集，经过20轮的训练，最终成绩分别是81.95与84.45。

项目地址：https://github.com/ghost-him/study/tree/main/catvsdog

思考题

Residual learning 的基本原理？

在传统的深度神经网络中，通常是将一层的输出直接作为下一层的输入。而在残差神经网络中，每一层的输出是由该层的输入与该层学习到的残差的和。可以通过$y=F(x,{W_{i}})+x$表示。$x$为输入，$F(x,{W_{i}})$为学习的残差映射，${W_{i}}$为学习参数,$y$为输出。特点是由多个残差块组成，而一个残差块包含2个或3个卷积层，还有一个跳跃连接。

Batch Normalization 的原理，思考 BN、LN、IN 的主要区别。

BN层是用于手动将每一层的输出进行归一化处理，将输出调整为均值为0，标准差为1的正太分布。

BN的具体步骤如下：

  1. 计算均值
  2. 计算方差
  3. 归一化
  4. 缩放与平移（这里设置了两个可以学习的参数：$\gamma$与$\beta$，作用分别是控制缩放与平移）

可以从以下图看到，使用BN层以后，可以减少大量的浪费的数据（以sigmoid函数为例）

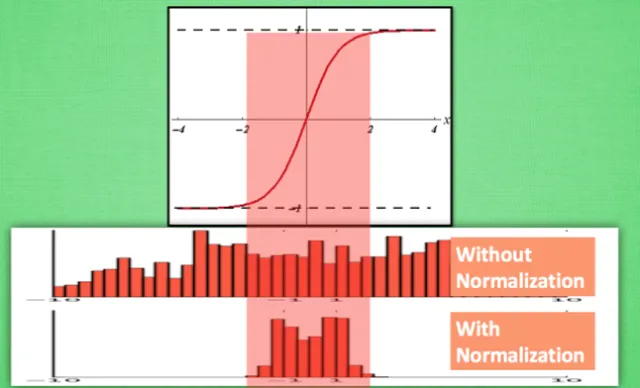
  • BN是在一个批次的数据上进行归一化，它计算每个特征维度在所有样本上的均值和方差。通常用于卷积神经网络的中间层。
  • LN是在每个样本上进行归一化，即对每个样本的所有特征维度计算均值和方差。适用于循环神经网络和Transformer模型。
  • IN是在每个样本的每个特征维度上进行归一化，即对每个样本的每个特征计算均值和方差。主要用于风格迁移等图像处理任务。

BN与IN：如果对一个图像进行归一化处理，则BN会计算整个批次中所有图像的红色通道的均值和方差，然后使用这些统计量来归一化批次中所有图像的红色通道的像素值。而IN则是分别计算每个颜色通道的均值和方差，然后使用这些统计量来归一化该通道的所有像素值。

为什么分组卷积可以提升准确率？既然分组卷积可以提升准确率，同时还能降低计算量，分组数量尽量多不行吗？

分组卷积允许每个组专注于不同的特征子空间，这种操作可以使模型更好的捕捉到多样化的特征信息。可以在不改变模型的计算复杂度的情况下，显著提升模型的表现。

分组数量过多时，对准确率的提升几乎没有作用，同时还会大幅度增加模型的训练时间，因此不可以过多。比如：当在32组的基础上再增加32组，准确率可能只会提升0.1%，但是训练花费的时候却可能增加50%。

附加题

Res2Net

模型改进

Res2Net改进了ResNet的残差块的结构，从而实现了多尺度卷积。

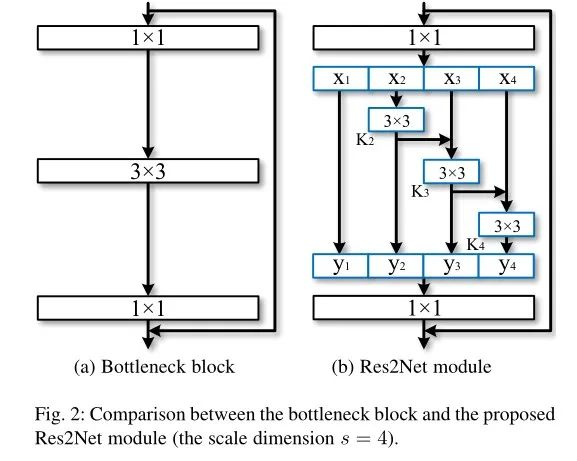
上图将一个输入的数据分成了 4 份（在实际的操作过程中也可以将其分成多份）。以 $x_{2}$ 为数据为例：该数据经历了 1 个 3*3（y2），一个 2 份 3*3（y3），一个 3 份 3*3（y4），其特征表示一定会比左侧只有一个 3*3 的卷积好。

这种结构的设计实现了多尺度的卷积：小的感受野可能会看到更多的物体的细节，对于检测小目标有很大的好处；而大的感受野可以感受物体的整体结构，方便网络定位物体的位置，细节与位置的结合可以更好的得到具有清晰边界的物体信息。

比较 multi-head 和 分组卷积 的区别与联系

联系：它们都是将一个整体拆分成了多个独立的子空间，然后在子空间中独立的计算，最后再拼接起来，并进行线性变换。它们都可以通过减少计算量来提高效率。

区别：multi-head主要用于NLP领域的自注意力机制（self-attention）中，而分组卷积主要用于CNN中。