Enhanced Spatiotemporal Prediction Using Physical-guided And Frequency-enhanced Recurrent Neural Networks

发表于 2024-08-23

论文地址：arxiv

摘要

该论文提出了一种物理引导的神经网络，它利用频率增强的傅里叶模块与矩损失来增强模型预测时空动态的能力。此外，还提出了一种具有特惠约束的自适应二阶龙格-库塔（Runge-Kutta）方法，以更精确地建模物理状态。

正文

创新点

受到 Transformer 与 FNO 方法的启发，将两个主要信息通路神经网络中，包括基于傅里叶块的通路用于空间信息处理，以及基于 Transformer-LSTM 的另一条通路用于时间信息处理。
设计了一个自适应二阶龙格-库塔模块 (ARKM)，在接收两条通路的时空信息后进行物理状态估计。ARKM 模块包含一个自适应门控机制和 PDE 引导的卷积，以及总损失函数中的一致性矩（congruent moment）损失。
使用高频主导的 H 1 损失来捕捉通常在 PDE 信息神经网络中被忽视的高频特征，以很好地表示动态边界。此外，将频域 H 1 损失与 MSE 损失和上述矩损失相结合，强制网络学习空间频率和时间导数。

模型架构

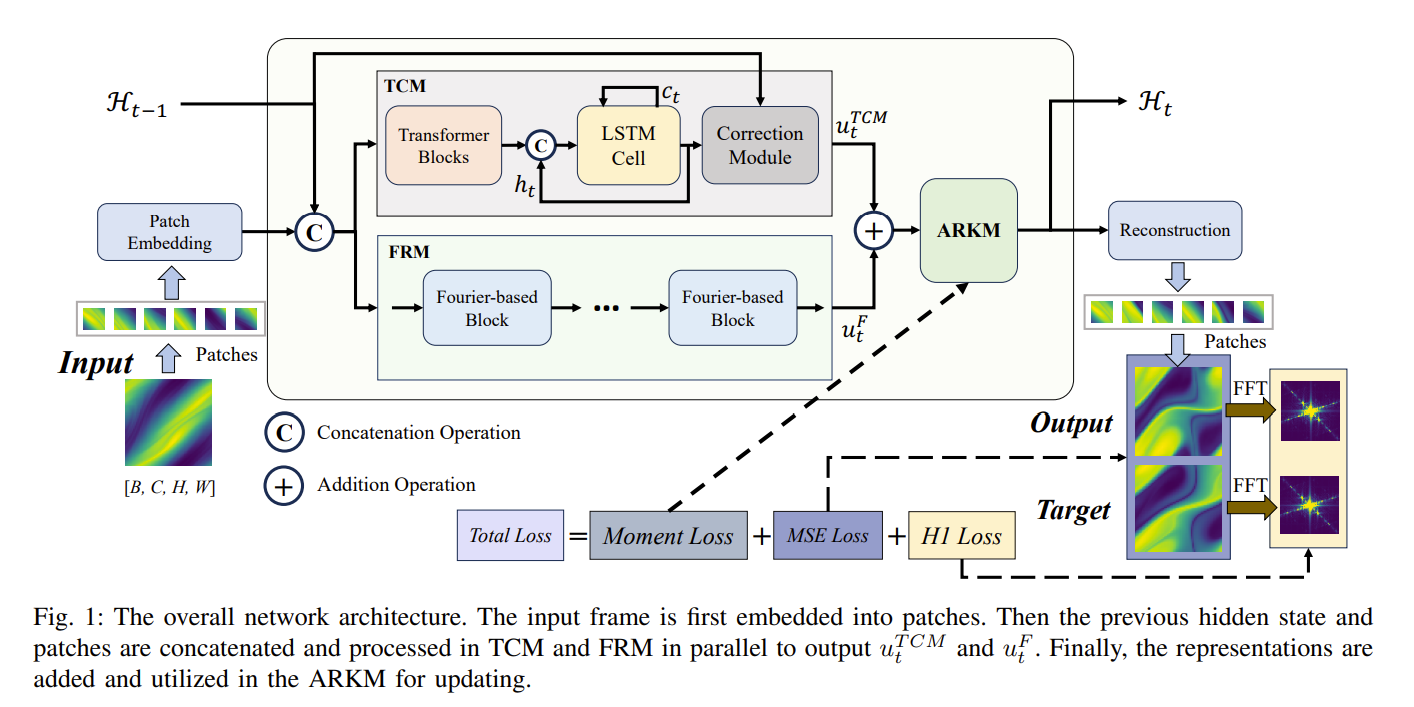
该模型将三个组件整合到了一个循环单元中：

基于 Transformer 的 LSTM 单元修正模块（TCM），用于建模一般的空间依赖关系
基于傅里叶变换的残差模块（FRM），用于学习物理表示
自应用二阶龙格-库塔模块 (ARKM), 用于物理状态估计和迭代

MSE 损失、H 1 损失和矩 (moment) 损失构成了训练损失函数。

模型的输入为：过去帧序列 ${x_1,…,x_T}$。其中 $x_t \in R^{CHW}$ 是时间步 t 的观测值。$C$，$H$，$W$ 分别是输入帧的通道数，高度和宽度。$T$ 是输入序列的长度。模型的目标是通过最小化预测帧和真实帧之间的差异来预测未来序列 $\hat{x}{T+1},…,\hat{x}{T+T’}$，其中，$\hat{x}t$ 表示时间步的模型预测值，$T’$ 是预测范围。具体来说，由于模型是递归训练的，它将当前帧 $x_t$ 作为输入并预测下一帧 $\hat{x}{t+1}$。在推断未来序列时，模型将预测帧作为下一步的输入。

作者先使用块嵌入（patch embedding），将输入帧 $x_t$ 嵌入为 $u_t$，之后使用两个并行分支来建模潜在空间：

使用 transformer 块与 LSTM 单元分别提取一般空间特征与修正隐藏空间
使用傅里叶块以物理引导的方式增强空间依赖关系

然后将输出的结果相加，后使用自适应龙格-库塔模块进行更新。

U^T_t = \text{Transformer Blocks}((u_t; H_{t-1}))

U^{TC}_t = \text{LSTMCell}(u^T_t, h_t, c_t)
$$

$$
U^{TCM}_t = \text{Correction Module}(u^{TC}t, H{t-1})
$$

$$
U^F_t = \text{FRM}((u_t; H_{t-1}))
$$

$$
H_t = \text{ARKM}(u^F_t + u^{TCM}_t)

$$
其中，$(.;.)$ 表示连接操作。最后，更新后的隐藏状态 $H_t$ 被重建为预测 $x$。

基于 transformer 的校正模块（TCM）

Vision Transformer中实现的全局多头自注意力（MHSA）机制计算所有标记之间的相关性，从而提高了空间相关性的表示能力。而Swin Transformer提出了基于窗口的多头自注意力（W-WHSA）和基于移动窗口的多头自注意力（SW-WHSA），以减少计算开销并增强建模性能。

Swin Transformer 的结构如下：

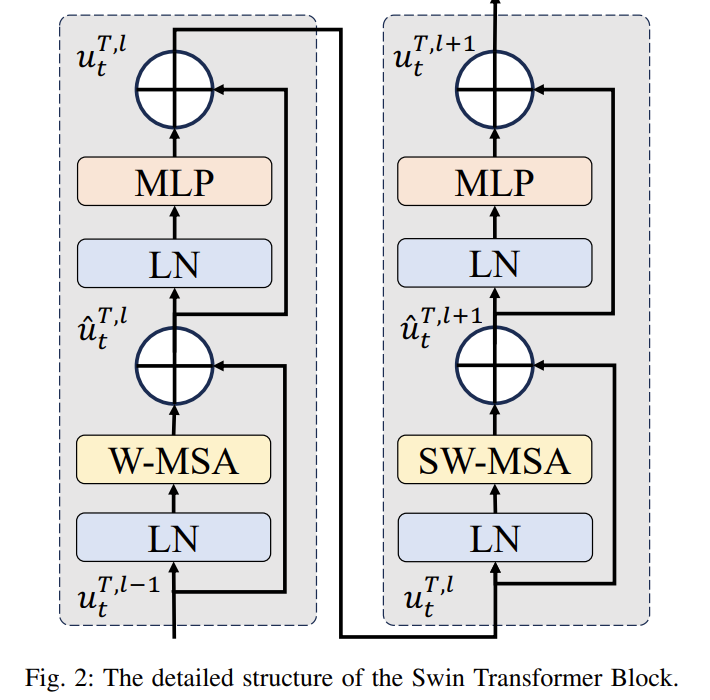
虽然 Swin Transformer 块用于提取空间相关性，但是每个时间步的瞬态变体不仅依赖于空间上下文，还表现出显著的时间一致性。为了建模时间一致性，作者采用了LSTM单元来学习瞬态变化。

最后，隐藏状态通过校正模块根据当前输入特征进行调整，以提高精度。

傅里叶残差模块（FRM）

该模块的结构如下：

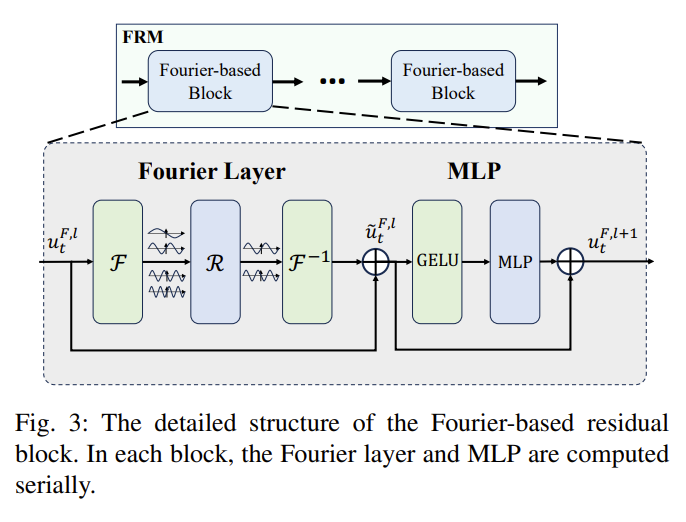
该模块旨在通过物理引导的数据驱动方式增强由基于 Transformer 的校正模块学习到的特征。傅里叶模块由傅里叶层和多层感知器（MLP）组成。傅里叶层利用快速傅里叶变换（FFT）和逆快速傅里叶变换（IFFT）在频域中使用可学习的核直接建模映射函数。

在每个模块中，首先对输入标记应用二维FFT，然后训练一个由实部和虚部参数化的核 $R_{\phi}$ 与 $Z^l_t(u,v)$ 相乘，以在傅里叶域中计算。最后，将混合标记从傅里叶域转换到空间域，使用二维IFFT。

残差连接与 MLP 被添加到傅里叶层以稳定训练过程，确保模型的有效性与稳定性。同时使用编码器层的嵌入块作为输入。

自适应龙格-库塔模块（Adaptive Runge-Kutta Module, ARKM）

为了以偏微分方程指导的方式更新两个分支模块表示的隐藏状态，作者设计了一个自适应二阶龙格-库塔方法的更新模块来更新隐藏状态。龙格-库塔方法通常用于神经网络的更新。

在传统的 RK 2 方法中，作者发现有可能会在块数较多时导致梯度消息。所以为了解决梯度消息问题，适应递归模型中的门机制，并提高模型性能。作者设计了一种自适应 RK 2 方法，通过自动学习系数以数据驱动的方式缩放 $h_{t+\Delta t}$ 与 $h_{t+ 2 \Delta t}$。基于这个想法，利用加权门机制来缩放。其中，加权门由卷积核大小为 1*1 的卷积 $W_g$ 与偏置 $b_g$ 计算。

该模块的详细结构的架构如下所示：

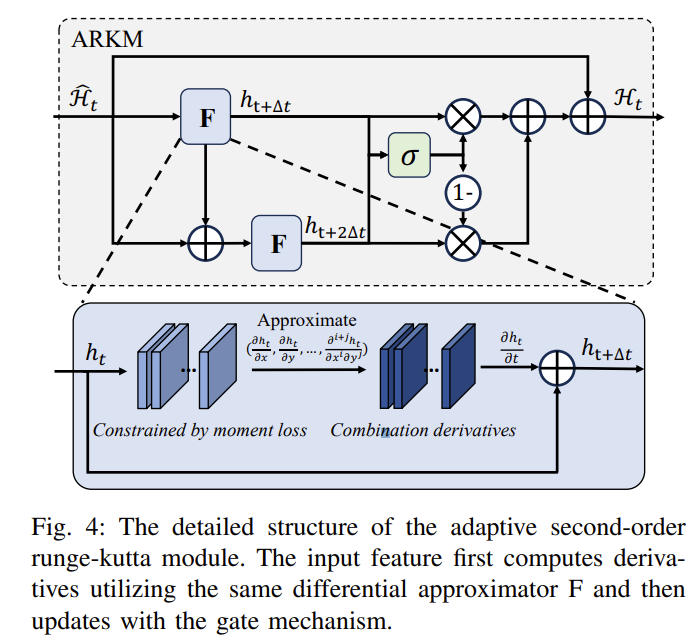
信息召回机制

考虑到编码中信息丢失的问题，作者在编码器与解码器之间利用信息召回机制来增强模型的重建能力。将补丁嵌入层（patch embedding layers）分为若干子补丁嵌入层。例如，如果补丁大小为 4*4，我们将补丁嵌入层分为两个 2*2 的卷积层，其卷积核大小和步长均为 2。补丁重建层（patch reconstruction layers）也采用相同的操作。

损失函数

在实验中，使用以下损失来优化模型：

$$
L=L_{prediction} + \lambda_m L_{moment}
$$
预测损失 $L_{prediction}$ 包含了两个损失，即均方误差（MSE）损失与 H 1 损失，可以表示为 $L_{MSE}+\lambda_HL^{H1}$。

在视觉任务中，关键信息包含在对象的边界或高对比度的像素中，这对应于频域中高频信息。所以引入了频域 H 1 损失来强调图像中的高频成分。$L^{H1}$ 的细节为：

$$
L^{H^1}(\hat{x}, y) := \sqrt{\sum_{\xi=-N/2+1}^{N/2} (1 + 4\pi^2 |\xi|^2) |F(\hat{x})\xi - F(y)\xi|^2}
$$

在 H 1 损失中，在求和中引入了一个与 $|\xi|^2$ 成比例的项，其中 $\xi$ 表示频率。通过引入这一项，H 1 损失可以被解释为一个强调高频成分的加权 L 2 损失。

为了使自适应 RK 2 模块中的卷积网络逼近空间导数，施加矩量损失 $L_{moment}$ 来约束卷积的权重。

其公式如下：

$$
L_{moment} (W_p) = \sum_{i \leq k} \sum_{j \leq k} L^2 M(W^k_{p,i,j}) , M^k_{i,j}
$$

矩矩阵（moment matrix）

可以通过卷积滤波器来近似偏导数。其核心思想是使用矩矩阵来约束滤波器，使其可以近似特定的微分算子。矩矩阵的每个元素通过滤波器的权重与位置的幂次来定义。
通过对矩矩阵施加特定的约束，可以使滤波器专注于近似特定的微分阶数，从而实现对微分算子的近似。

实验

以下是基准的详细信息

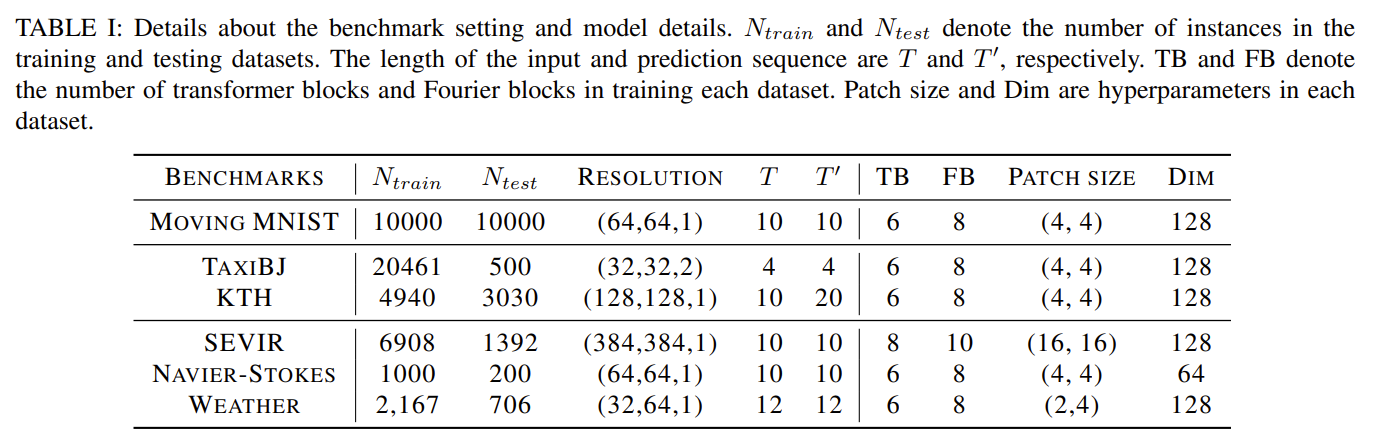
以下是模型在基准上的表现：

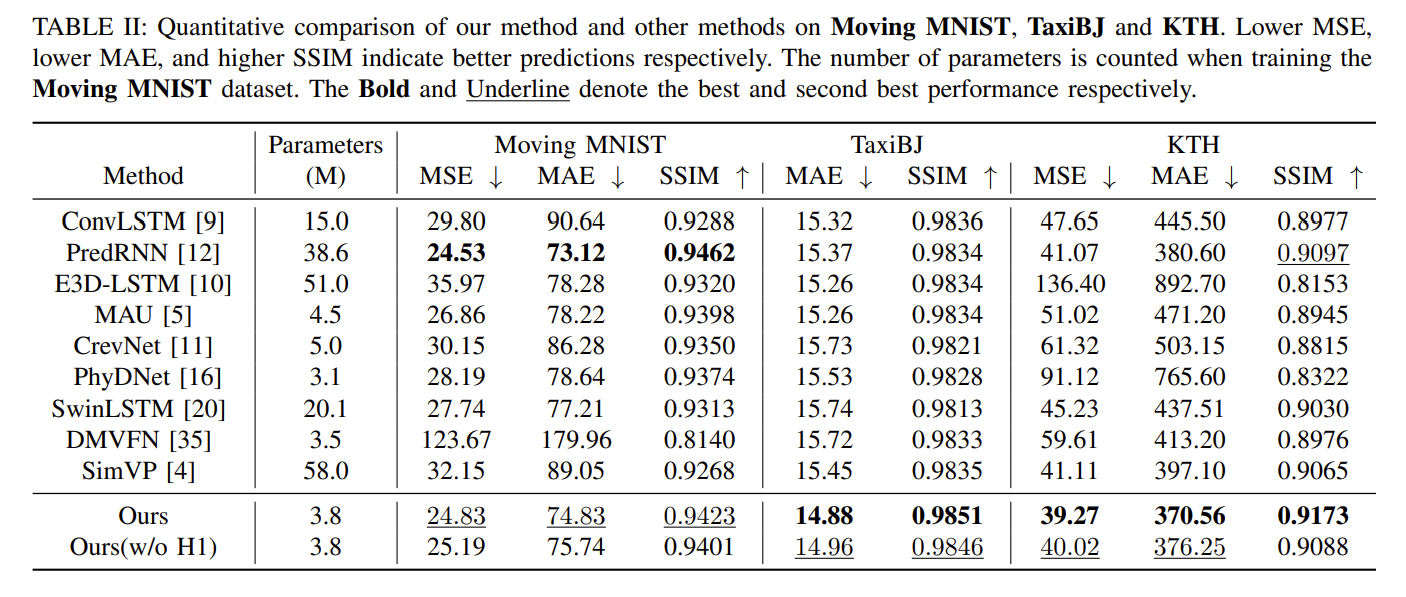
模型在 TaxiBJ 和 KTH 数据集中表现最佳，在 Moving MNIST 数据集中表现第二。同时，模型的参数远小于 SOTA 方法 PredRNN、SimVP 和 SwinLSTM。

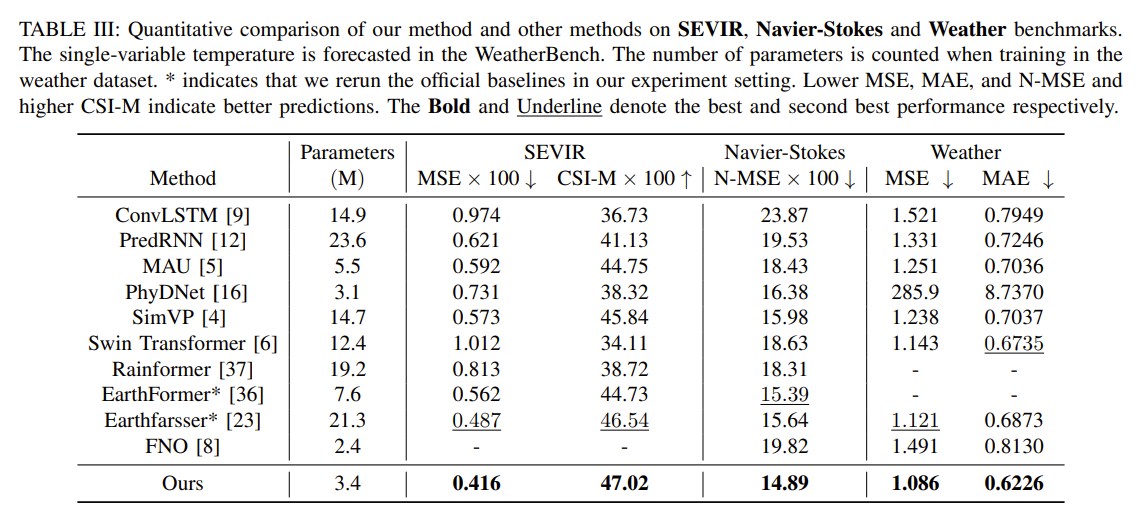
模型在所有自然动态现象中表现最佳，在这些数据集上实现了最低的 MSE，MAE，和最高的 CSI-M。

消融实验

Patch 大小

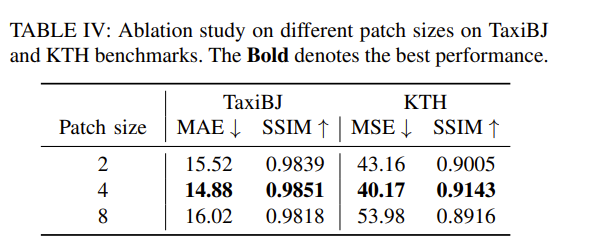
最佳Patch大小可能因数据集而异，但4×4的大小通常效果良好。

解码器层

解码器层用于将隐藏表示解码为目标输出图像。有许多方法可以对表示进行上采样。

作者设计了两种方法：ConvTransposed2D和双线性插值（Bilinear Interpolation），这两种方法是常用的视觉任务。

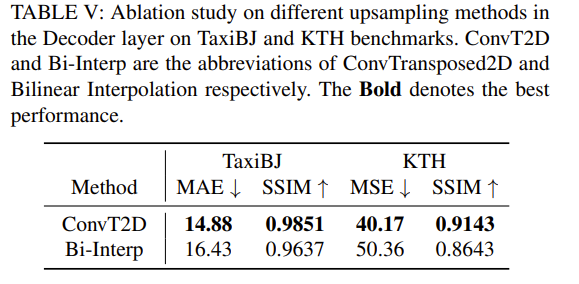
可以看到，ConvTransposed2D方法比双线性插值方法效果要好得多。

Transformer和Fourier模块的数量。

每个模块中的块数量极大地影响模型的学习能力和参数数量。由于计算资源的限制，作者将Transformer块的数量固定为8或Fourier块的数量固定为10。

同时，为了评估模块的有效性，作者也做了消融研究，包括移除组件（w/o）和用其他组件替换（rep）。

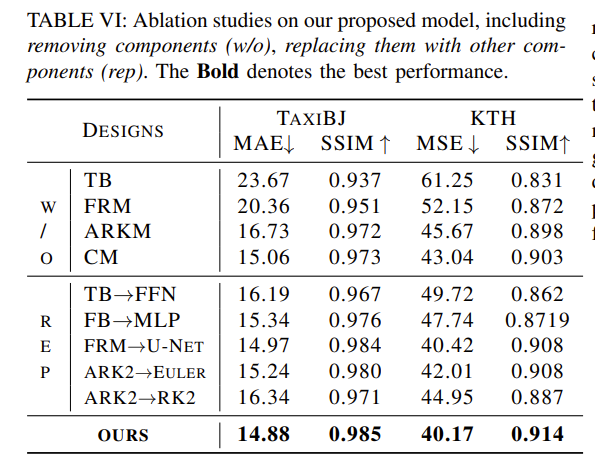
结果显示，

在移除（w/o）实验后，模型的所有组件对于时空预测都是必不可少的。特别是，没有Transformer块和Fourier模块，模型性能会严重下降。
在替换实验中也可发现类似结果，Transformer块和Fourier块明显优于FFN和MLP。作者认为，这是因为Transformer和Fourier层在建模空间相关性方面具有更强的能力。
将基于Fourier的残差模块替换为U-Net可以获得类似的性能，但使用U-Net时参数数量会大得多。
自适应RK2模块比传统的Euler和RK2方法要好，参数的增加很小。