MIMO Is All You Need -- A Strong Multi-in-Multi-Out Baseline for Video Prediction
论文地址:arxiv
摘要
大部分模型都是基于 SISO,所以作者想要探索 MIMO 架构的能力。
作者研究后发现,MIMO 模型可以以远超预期的大幅度优势超越最先进的工作,尤其是在处理长期误差累积方面。所以作者提出了基于纯 transformer 与局部时空块和新的多输出解码器,名字为 MIMO-VP。
正文
传统模型的问题:早期的小误差在后期会被不断放大,从而导致准确性与质量迅速下降。尤其是非结构化的视频数据,比如天气,雷达视频等。而模型的改进也只是减少一次生成的来缓解问题,没有打破误差传播链。
同时,原始Transformer模型只会导致较差的模型性能,因为它们难以利用视频的两个非常重要的线索 - 每一帧的空间依赖性和复杂的时空动态。
- 对于全局时空依赖性线索,作者将 2 D 卷积整合到多头注意力机制中,以同时捕捉序列的长期时间依赖性并保留帧的空间信息。
- 对于时空线索,作者设计了一个时空块,用来替换编码器与解码器中的简单前馈层。这个块将捕捉局部时空上下文以有利于预测。
由于典型的 Transformer 的解码器无法直接实现 MIMO,作者设计了一个新的多输出解码器,它将所有输出帧的占位符作为输入特征。然后最后一层以一次性生成输出帧。
贡献
- 表明多输入多输出策略在解决视频预测中长期存在的误差累积问题中起着至关重要的作用。
- 提出了新的 MIMO 架构,通过利用视频数据的空间上下文与局部时空相关性来改进基于 Transformer 的架构(Transformer 有着建模长期依赖性的优势)。
问题表述
给定一个视频序列 $S_{t-m+1: t} := {X_{t-m+1},…,X_{t}}$,其中 $X_{t} \in R^{C_0H_0W_0}$ 表示在当前时间步 $t$ 的帧(通道数为 $C_0$,高度为 $H_0$,宽度为 $W_0$)。时空序列预测的目标是,在给定之前的长度为 $m$ 的序列的情况下,生成未来最可以的长度为 $n$ 的序列。
$$
S^*_{t+1:t+n} = \arg \max_{S_{t+1:t+n}} p(S_{t+1:t+m} \mid S_{t-m+1:t})
$$
MIMO 预测的策略
$$
S_{t+1:t+n} = F(S_{t-m+1:t}) + \Sigma_{t+1:t+n}
$$
其中,$\Sigma_{t+1:t+n} :={\sigma_{t+1},…,\sigma_{t+n}}$ 是正常预测误差。
由于 MIMO 模型可能会错过一些 SISO 模型自然捕捉到的重要关系,单帧的误差可能会非常高。同时,为其配备强大的建模长短期时空依赖性的能力也不容易。
模型结构
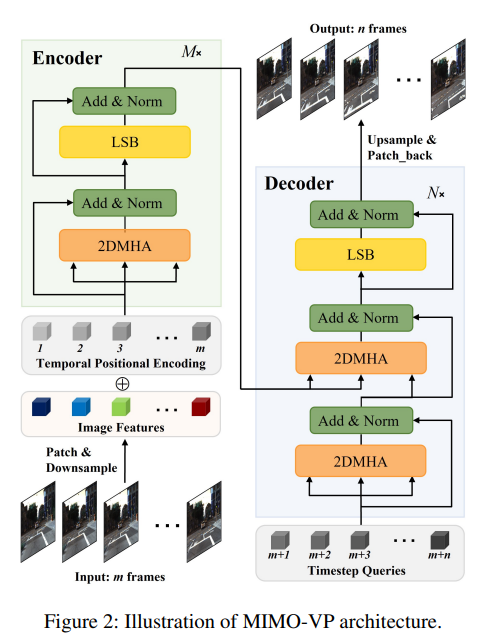
模型的公式为:
$$
S_{t+1:t+n} = \Phi_d(\Phi_e(S_{t-m+1:t}), T_{t+1:t+n})
$$
$\phi_d$ 与 $\phi_d$ 分别是编码器与解码器模块。$T_{t+1:t+n}$ 是长度为 $n$ 的时间步查询。对于输入视频 $S_{t-m+1: t} \in R^{mC_0H_0W_0}$ 具有 m 帧,先将每帧分解为不重叠的块,然后经过若干卷积层获得序列级特征图 $h \in R^{mCHW}$。
注意点:首先操作 2 D 卷积多头注意力(Multi-Head Attention, MHA)以生成每帧的查询图与配对的键值图。这有助于模型同时学习时间相关性并保留序列的空间信息。此外,在解码器块中没有对多头自注意力应用掩码操作(解码器输入是已知的时间步嵌入)。在该模型中,每个生成的帧不仅依赖于过去的序列,还依赖于其未来的帧,从而保留了未来帧的依赖性。
局部时空块(Local Spatio-Temporal Block)
局部时空块可以捕捉序列短期变化,这对视频生成至关重要。它可以学习时间步查询 $T$ 与其对应输出序列 $S$ 之间的高阶关系。
在编码器与解码器的全连接层位置安装这个块就可以实现这个想法。理论上,可以捕捉视频数据时空信息的神经网络。
为了使这个块简单,作者使用了简单的 3 D 卷积层。所以,这个块由两个嵌入层组成,每个嵌入层是一个大小为 3*3*3 的 3 DConv,LayerNorm 和 SiLU 块。
多输出解码器(Multi-Out Decoder)
由于 Transformer 架构的排列不变特性,作者在这里专注于序列的时间位置编码:定义一个时间步向量 $T = [1, 2, …, m+n]$。然后,通过一个嵌入层将 $T \in R^{1*(m+n)}$ 嵌入到 $\hat{T} \in R^{(m+n)C}$。最后,将 $\hat{T}$ 沿高度与宽度维度扩展到 $T \in R^{m+n}CHW$。相应地,输入序列的时间位置编码为 $T_{1: m} \in R^{mCHW}$。之后将 $T_{m+1:m+n} \in R^{nCHW}$ 视为时间步查询并将其输入到解码器模块。
当输入长度为 1 时,单输入单输出(SISO)策略在某种程序上是多输入多输出策略的一个特例。
模型评估
使用的数据集:
- Moving MNIST
- Human 3.6 M
- 天气数据集
- KITTI 数据集
评估了均方误差(MSE)、平均绝对误差(MAE)、结构相似性(SSIM)、LPIPS(Zhang 等,2018)和峰值信噪比(PSNR)。所有这些指标均在所有预测帧中取平均值。
以下是 Moving MNIST 的定量与定性比较
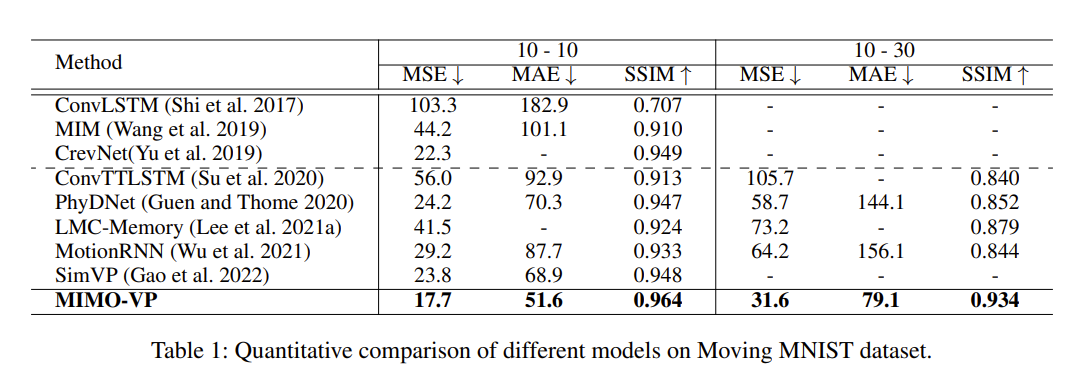
在 MSE 指标上远超其他模型。
以下是在 Human 3.6 M 上的结果
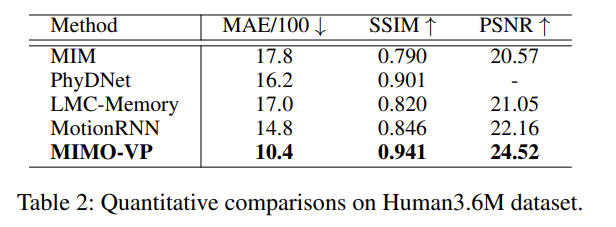
以下是 KITTI 的结果
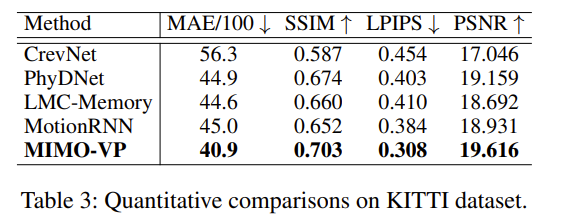
以下是在天气数据集上的结果
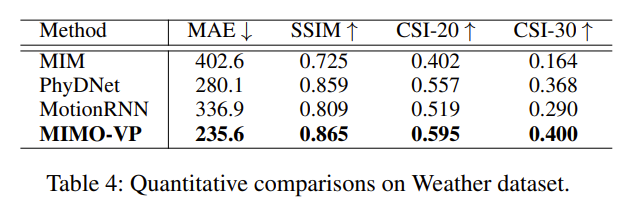
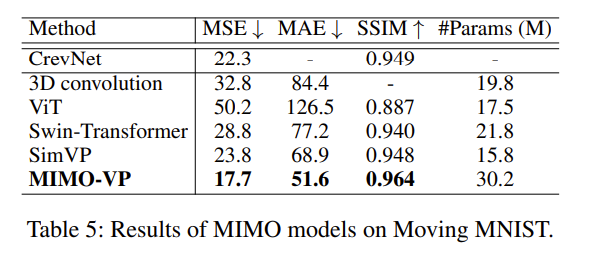
以下是对比其他的 MIMO 的结果:
消融实验
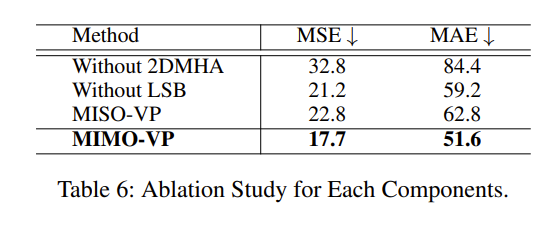
实验分别以下三个做了消融实验,证明了三者缺一不可:
- 帧的空间依赖性
- 局部时空块(LSB)
- 多输出解码器(删除后就变成了递归单输出预测策略)
多输入的重要性
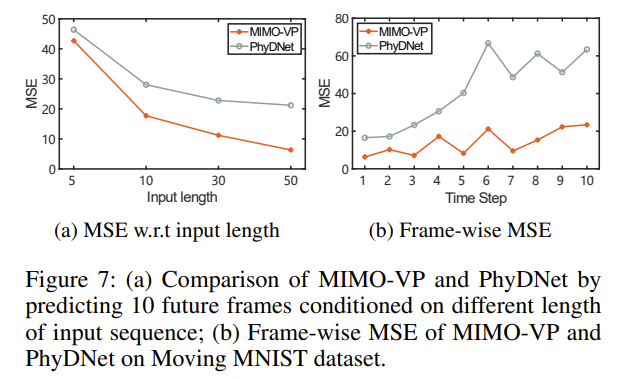
可以实现长期依赖性。从上图 a 可知,当输入的长度增加时,MSE 快速下降。并且下降幅度更快,表示在捕获视频序列的长期时空依赖性方面具有更强的能力,而基于 RNN 的 PhyDNet 由于内存容量有限而受到长期依赖问题的困扰。
多输出的重要性
可以实现无误差累积。从上图 b 可知,MIMO-VP 的曲线随时间只有轻微的上升。
同时为了验证误差累积问题在长期情况下更严重,做了以下的实验:在训练阶段,所有模型都使用 10 帧来预测接下来的 10 帧,而在测试阶段,以递归方式预测 10、30、50 和 90 帧。
结果如下:
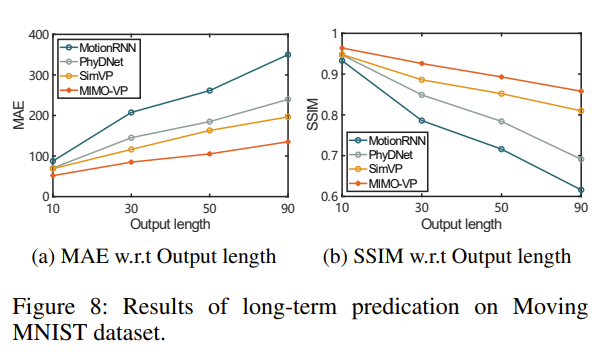
表明多输出模型可以克服视频预测中的误差累积问题。
未来帧依赖性
将 MIMO-VP 与其变体 MIMO-F 进行比较,后者是一个在解码器中去掉自注意力模块的基线,因此无法捕获所有帧的依赖性。
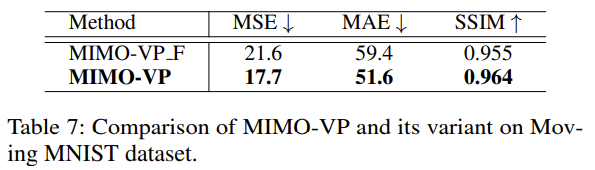
表明了 MIMO-VP 在保持未来帧之间的依赖性以进行准确预测方面的优势。