深度学习：算法到实战学习笔记01

笔记内容来源：视频

深度学习基础

深度学习的发展过程

计算机发展的三个智能层面

• 计算智能：能存储，会计算。解决问题的方法主要基于暴力穷举。
• 感知智能：拥有人类一样的视觉，听觉，触觉等感知能力。
• 谁知智能：计算机可以拥有概念，意识，观念。

人工智能与其他领域的结合

• 人工智能+金融：支付宝的芝麻信用
• 人工智能+内容创作：gpt
• 人工智能+机器人：机械臂

人工智能的应用

• 计算机视觉
  • 应用：人脸识别，图像分类，目标检测，图像分割等。
• 语音技术
  • 语音合成，声纹识别等
• 自然语言处理
  • 机器翻译，知识图谱等

人工智能，机器学习，深度学习的关系

人工智能 > 机器学习 > 深度学习

• 人工智能是一个领域，是一个目标。
• 机器学习是实现人工智能的一个方法。
• 深度学习机器学习众多方法中的一个方法。

实现人工智能的方法

ai 数理基础	逻辑：知识表达与推理	概率：模型，策略，算法
主流技术	逻辑推理，知识工程	机器学习
Ai 学派	符号主义（自上而下）	贝叶斯：对事件发生的可能性进行概率推理（自上而下+自下而上）；联结主义：模拟脑结构：使用概率矩阵来识别和归纳模式（自下而上+自上而下）
代表方法	定理证明机，专家系统	朴素贝叶斯，神经网络，隐马尔科

知识工程 vs 机器学习

• 知识工程：基于手工设计规则，结果容易解释，系统构建费时费力，难以保证一致性和准确性

• 机器学习：基于数据自动学习，结果可能不易解释，提高信息处理的效率，减少人工规则主观性，可信度高

专家系统

机器根据专家定义的知识和经验，进行推理和判断，从而模拟人类专家的决策过程来解决问题。

专家系统的缺点：定制一个专家系统耗时耗力，而且专家系统的准确度完全依赖于人类专家。

常见的专家系统有：调查问卷

在定制专家系统时，对于每一个问题，都要确定其语义概念；对于一个问题的选项，要确定其对于目标问题的含义。

机器学习

定义

• 常用定义：计算机系统能够利用经验提高自身的性能
• 可操作定义：机器学习本质是一个基于经验数据的函数估计问题
• 统计学定义：提取重要模式，趋势，并理解数据，即从数据中学习

机器学习学的是有意义的模式，有规律的模式，比如：预测天气，预测比赛获胜的概率；而不是无意义的模式，比如：下一次抛硬币是正面还是反面。

机器学习的三要素

模型

模型是机器学习系统的核心，它是用来表示数据和预测结果之间关系的数学结构或函数。模型可以看作是一个函数，它接受输入数据并输出预测结果。

常见的模型有：

• 线性模型：线性回归，逻辑回归。
• 非线性模型：决策树，支持向量机，神经网络。
• 概率模型：高斯混合模型，隐马尔可夫模型。

模型的作用是从数据中学习到有用的模式或规律，并能够对新的数据进行预测或分类。

在pytorch中，模型代表神经网络的模型。

模型可以分为以下几种类别：

• 以数据标记分类
  • 监督学习模型
  • 无监督学习模型
  • 半监督学习
  • 强化学习
• 以数据分布分类
  • 参数模型
  • 非参数模型
• 以建模对象分类
  • 判别模型
  • 生成模型

监督学习模型：样本具有标记。从数据中学习标记分界面，适用于预测数据标记

无监督学习模型：样本没有标记。从数据中学习模式，适用于描述数据。

半监督学习模型：部分数据标记已知。是监督与无监督学习的混合。

半监督学习模型的出发点是标记样本难以获取，无标记样本相对廉价。因此，其假设未标记样本与标记样本独立同分布，包含关于数据分布的重要信息。（聚类假设与流形假设）

强化学习模型：数据标记未知，但知道与输出目标相关的反馈。适用决策类问题。

强化学习模型会使用未标记的数据，但可以知道离目标越来越近还是越来越远（奖励反馈）。

参数模型：对数据分布进行假设，待求解的数据模式可以用一组有限且固定数目的参数进行刻画。例：线性回归模型。

非参数模型：不对数据分布进行假设，数据的所有统计特性都来源于数据本身。例：k 近邻，决策树，随机森林。

在参数模型与非参数模型中，

• 参数是指数据分布的参数，而不是模型的参数。
• 非参数模型的时空复杂度一般比参数模型大得多。
• 参数模型的模型参数固定，非参数模型是自适应的，模型参数随样本变化而变化

	参数模型	非参数模型
优点	数据需求少，训练快速	对数据适应性强，可以拟合不同的函数形式
缺点	模型复杂度有限，与真实目标函数拟合度小	数据需求大，容易过拟合

判别模型：输入特征 X，直接预测出最可能的 Y。专注于区分不同类别的数据。例：SVM，逻辑回归，条件随机场，决策树。

生成模型：对输入 X 与输出 Y 的联合分布 $P(X,Y)$ 建模。这种模型不仅可以进行分类，也可以生成类似于训练数据的新数据。例：朴素贝叶斯，隐马尔可夫，马尔科夫随机场。

策略

策略，也称为目标函数或损失函数，是用来评估模型性能的标准。它定义了模型输出与实际结果之间的差异，并指导模型的优化过程。

常见的策略有：

• 均方误差：用于回归问题，衡量预测值与真实值之间的平均平方差。
• 交叉熵损失：用于分类问题，衡量预测概率分布与真实分布之间的差异。
• 二元交叉熵损失：用于二分类任务，计算二元交叉熵损失。

损失函数的作用是量化模型的预测误差，并通过最小化损失函数来优化模型参数，从而提高模型的预测准确性。

在pytorch中，策略代表使用的损失函数。

• 策略设计
  • 无免费午餐定理
    • 当考虑在所有问题上的平均性能时，任意两个模型都是相同的：脱离了具体的问题，则无意义
    • 没有任何一个模型可以在所有的学习任务里表现最好
  • 奥卡姆剃刀原理
    • 如无必要，勿增实体：简单有效原理
    • 如果多种模型能够同等程度地符合一个问题的观测结果，应该选择其中使用假设最少的那个

算法

算法是指优化模型参数的具体方法或步骤。它是训练模型的过程，通过不断调整模型参数来最小化损失函数。

常见的算法有：

• 梯度下降：一种迭代优化算法，用于最小化损失函数。例如：随机梯度下降（SGD）。
• 牛顿法：一种二阶优化算法，利用损失函数的二阶导数信息进行优化。
• 遗传算法：一种基于自然选择和遗传机制的优化算法，适用于复杂的优化问题。

算法的作用是通过优化过程。

在pytorch中，算法代表使用的优化器。

传统机器学习与深度学习

传统机器学习

特点：人工设计特征。

处理流程：

1. 预处理：经过数据的预处理，如去噪声等。（人工）
2. 特征提取：从原始数据中提取一些有效的特征。（人工）
3. 特征转换：对特征进行一定的加工，比降维与升维。（人工）
4. 预测识别（机器）

深度学习

处理流程：

1. 输入
2. 浅层的特征（机器）
3. 深层的特征（机器）
4. 预测识别（机器）

频率学派与贝叶期学派

频率学派

• 关注可独立重复的随机试验中单个事件发生的频率
• 可能性：可作发生频率的极限值->重复试验次数趋近于无穷大时，事件发生的频率会收敛到真实的概率
• 假设概率是客观存在且固定的
• 模型参数是唯一的，需要从有限有观测数据中估计参数值

方法：统计机器学习：设计不同概率模型去拟合数据背后的规律->用拟合出的规律去推断和预测未知的结果（线性回归，决策树，支持向量机）

贝叶斯学派

• 关注随机事件的可信程序，如天气预报明天下雨的概率
• 可能性：假设+数据：数据的作用是对初始假设做出修正，使观察者对概率的主观认识更接近客观实际
• 模型参数本身是随机变量，需求估计参数的整个概率分布

方法：概率图模型：根据数据+变量的先驱分布，同时推断每个变量以及变量之间关系的后验分布（隐马尔科夫，条件随机场，主题模型）

Beyond 深度学习

统计机器学习：寻找相关性

但是，相关性不可靠：Yule-Simpson 悖论。相关关系可能由于 context 等混杂因素而改变。

相关性与因果性：因果性=相关性+忽略的因素。

因果性：排队其他因素后，Y 仅由 X 影响
相关性：Y 发生时往往伴随着 X

• 群体智能

例：在看验证码，图像检测，图像分割

深度学习的“不能”

算法输出不稳定，容易被”攻击”

• 模型复杂度高，难以纠错与调试
• 模型层级复合程序高，参数不透明
• 端到端的训练方式对数据依赖性强，模型增量性差
  • $Test loss - training loss <= \sqrt{\frac{N}{m}}$
  • m: 训练样本，N：模型有效容量
  • 当样本数据量小的时候，深度学习无法体现强大的拟合能力
• 专注直观感知类问题，对开放性推理问题无能为力
• 人类知识无法有效引入进行监督，机器偏见难以避免
  • 算法依赖于大数据，但数据不是中立的：来源社会，存在不平等

解释性的三个层次

1. 找得到：出了问题可以快速纠错
2. 看得懂：双向：算法可以被人的知识体系理解+利用和结合人类的知识
3. 留得下：越学越聪明

评估机器学习的两个维度

• 准确性
• 解释性

当前，深度学习的准确性很高，解释性很低。

提高解释性的可能的方法：

• 深度学习+图谱
• 数据+知识

浅层神经网络

M-P 神经元

• 多输入信号进行累加 $\sum_{i}x_{i}$
• 权值 $w_{i}$ 正负模拟兴奋\抑制，大小模拟强度
• 输入和走过阈值 $\theta$，神经元被激活 (fire)
• 输出 $y = f(\sum_{i=1}^{n}w_{i}x_{i}-\theta)$
• 其神经元的权重预先设置，无法学习

激活函数 f

神经元继续传递信息，产生新连接的概率（超过阈值被激活，但不一定被传递）

如果没有激活函数，相当于矩阵相乘：多层与一层一样，只能拟合线性函数。

常见的激活函数：

• 线性函数
• 斜面函数
• 阈值函数
• 符号函数
• sigmoid 函数 （s 函数）

Sigmoid 函数

$$
\sigma (z)= \frac{1}{1+e^{-z}}
$$

缺点：

1. 容易饱和
2. 输出不对称（只能输出在 (0, 1) 之间）

针对第一个问题，提出了 ReLU 修正线性单元
针对第二个问题，提出了双极 S 性函数（tanh）

双极性 S 函数 (tanh)

$$
tanh(x)=2sigmoid(2x)-1=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}
$$

该函数的输出可以出现在 (-1, 1) 之间

ReLU 修正线性单元

$$
relu(z)=max(0,z)
$$

优点：当输入大于 0 时，其斜率可以保持为 1
缺点：当输入是一个很大的负值时，其结果永远是 0，无法输出一个正值。此时，相当于神经元已经失效了。

对于该缺点，提出了 Leaky ReLU 函数

Leaky ReLU

$$
leakyrelu(z)=max(0.01z,z)
$$

负轴不恒为 0，可以让其跳出负值。

单层感知器

• 单层感知器是首个可以学习的人工神经网络

• 单层感知器被证明，无法解决异或问题。

深层神经网络

多层感知器

通过组合单层感知器，即可得到多层感知器。

万有逼近定理

如果一个隐层包含足够多的神经元，三层前馈神经网络（输入，隐层-输出）能以任意精度逼近任意预定的连续函数。

线性分类任务组合后可以解决非线性分类任务的原因：第一层感知器将输入进行空间变换，将变换后的图像输入给第二层，第二层看到的就成了一个线性可分的问题。

• 双隐层感知器逼近非连续函数：当隐层足够宽时，双隐层感知器（输入-隐层 1-隐层 2-输出）可以逼近任意非连续函数：可以解决任何复杂的分类问题。

结构	决策区域类型	异或问题
无隐层	由一超平面分成两个	无
单隐层	开凸区域或闭凸区域	可以解决，但是要求分界面是连续的
双隐层	任意形状（其复杂度由单元数目确定）	可以解决，分界面也可以是不连续的

神经网络每一层的作用

每一层的数学公式
$$
\vec{y}=a(W* \vec{x}+b)
$$
完成：

• 升维/降维（$W*x$）
• 放大/缩小（$W*x$）
• 旋转（$W*x$）
• 平移（$+b$）
• 弯曲（$a()$）

训练数据的作用：让神经网络去选择一种线性或非线性的一种变换。

• 神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类/回归。
• 增加节点数：增加维度，即增加线性转移能力。
• 增加层数：增加激活函数的次数，即增加非线性转移次数。

宽度与深度

• 在神经元总数相当的情况下，增加网络深度可以比增加宽度带来更强的网络表示能力：产生更多的线性区域

• 深度和宽度对函数复杂度的贡献是不同的，深度的贡献是指数增长的，而宽度的贡献是线性的。

神经网络的参数学习：误差反向传播

• 多层神经网络可以看成是一个复合的非线性多元函数

$$
F(x)=f_{n}(…f_{3}(f_{2}(f_{1}(x)\theta_{1}+b)\theta_{2}+b)…)
$$

• 给定训练数据，希望损失尽可能小

训练的过程：输入一个数据，经过神经网络的逐层传播，得出一个结果，再和原本的输入做比较得出一个误差。再将该误差进行一个回传，再利用梯度来更新这个神经元。

梯度与梯度下降

导数：

• 函数值在某一点沿自变量正方向的变化率

• 多元函数在每个点可以有多个方向

• 每个方向都可以计算导数，这种导数称为方向导数。

梯度：

• 梯度是一个向量
  • 方向是最大方向导数的方向
  • 模为方向导数的最大值

无约束优化：梯度下降

• 参数沿负梯度方向更新可以使函数值下降
• 如果函数有多个极值点，则最终结果会非常依赖于初始点

反向传播算法（BP算法）

• 是训练多层前馈神经网络的核心方法。
• 整体网络的训练过程：通过前向传播计算输出，使用目标输出计算误差，然后通过反向传播计算梯度，最后更新权重和偏置。

多层神经网络的问题：梯度消失

训练神经网络的过程如下：

1. 前向传播：输入值 x 经过 w1，w2，…, wn 的计算后得到结果 c
2. 反向传播（误差通过梯度传播）

通过反向传播的更新公式为：

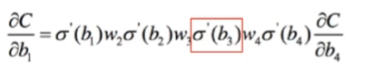
从该公式中可以知道：即使 $\frac{\partial C}{\partial b_{4}}$ 很大，但是前面相乘的值可能会很小（比如 sigmoid 函数接近 1 时的梯度），因此，结其最后的结果可能接近为 0，即出现梯度消息的情况。

因为存在梯度消息的问题，所以在训练多层神经网络时，往往是最后一层被训练的很好，但是第一层却几乎没变化。然而在最终做测试时，要使用所有层的网络。因为第一层没有被训练好，所以整体网络也没有被训练好。

增加深度会造成梯度消息，误差无法传播的问题；多层网络容易陷入局部极值，难以训练 ` => `三层神经网络是主流，预训练，新激活函数使深度成为可能

逐层预训练

原理：如果随机选择初始点会使得网络陷入不算很好的局部最优点，那么可以通过人为的选择一个不错的初始点来让网络达到一个很好的性能（即使其收敛的点不是全局最优点）。

优点：

1. 解会更加收敛一些，不容易进入一个很差的点里
2. 训练会更快

方式：

1. 先训练一层，等该层训练的差不多了以后，再加一层，该层则不再训练
2. 训练第二层，等该层训练的差不多了以后，再加一层，该层则不再训练
3. …
4. 训练完成

作用：

• 逐层无监督预训练使得深度网络的训练有了可能
• 其无法本质上解决梯度消失等问题

受限玻尔兹曼机和自编码器

目标：解决在逐层训练时中间的隐层看不到整体网络的输出结果的情况。

自编码器

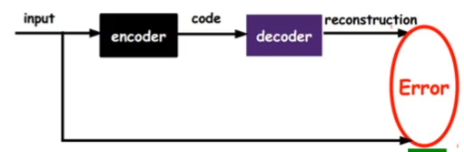
• 自编码器假设输出与输入相同，是一种尽可能复现输入信号的神经网络。

• 没有额外的监督信息：无标签数据，误差的来源是直接重构后信号与原输入相比得到的

• 自编码器一般是一个多层神经网络（最简单，三层）：

  • 训练目标是使输出层与输入层误差最小
  • 中间隐层是代表输入的特征，可以最大程度上代表原输入信号

• 自编码器最初用于降维，

使用自编码器构建深度神经网络

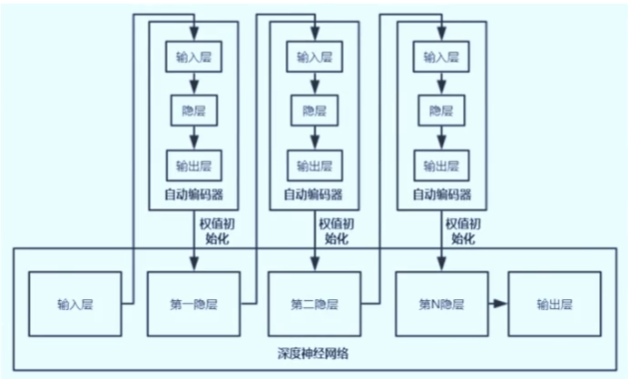
受限玻尔兹曼机

• 模型结构

  • RBM 是两层神经网络，包含可见层 v 与隐藏层 h
  • 不同层之间全连接，层内无连接，是一个二分图
  • 与感知器不同，RBM 没有旷工的重构过程：
    • 输入 V ，通过 p(h|v) 得到隐藏层 h；输入 h，通过 p(v|h) 得到 v
  • 目的是让隐藏层得到的可见层 v' 与原来的可见层 v 分布一致，从而使隐藏层作为可见层输入的特征
  • 两个方向权重 w 共享，偏置不同

• 条件概率建模

  • $p(h_{i}=1|v)=sigm(c_{i}+W_{i}v)$
  • $p(v_{j}=1|v)=sigm(b_{j}+W_{j}’v)$

获得概率模型的两种方法：

• 判别模型：直接对条件概率建模
• 深度模型：对联合概率做建模，然后使用 bs 公式算出条件概率

玻尔兹曼分布->sigmoid 激活函数证明：
$p(h|v)=\frac{P(h,v)}{P(v)}=…$

假设标准的玻尔兹曼分布中，所有的节点是二进制变量 (0, 1)，则
$$
P(h_{j}=1|v)=\frac{P(h_{j}=1|v)}{P(h_{j}=1|v)+P(h_{j}=0|v)}=…=sigmoid(b_{j}+W_{j}v)
$$

• 模型求解
  • 优化目标：网络表示的概率分布与输入样本分布尽可能接近
  • 可见层的 v 的似然：

深度信念网络 (DBN)

• 一个 DBN 由若干个 RBM 堆叠而成，最后加一个监督层
• 训练的过程由低到高逐层训练
• DBN vs DBM
  • DBM 没有监督层，是若干个 RBM 直接堆叠
  • 无向图模型，每两层互有反馈

一般玻尔兹曼机

• 可见层与隐层内部结点之间可连接
• 具有很强大的无监督学习能力，能够学习数据中复杂和规则
• 随机神经网络和递归神经网络的一种

缺点：

• 全连接图，复杂度很高

自编码器 vs 受限玻尔兹曼机

• 结构上
  • 自编码器编码和解码函数不同
  • RBM 共享权重矩阵 w，两个偏置向量
• 原理上：
  • 自编码器通过非线性变换学习特征，是确定的，特征值可以为任何实数
  • RBM 基于概率分布定义，高层表示为底层特征的条件概率，输出只有两种状态，用二进制表示
• 训练优化
  • 自编码器通过最损失函数 L 化重构输入数据，直接用 BP 优化求解
  • RBM 基于最大似然，能量函数偏导无法直接计算，基于采样方法进行估计
• 生成/判别模型：
  • RBM 对联合概率密度建模，是生成式模型；
  • 自编码器直接对条件概率建模，是判别式模型。

DNN

• 是前馈神经网络，训练方法是 BP
• 隐层激活函数使用 ReLU->改善梯度消失
• 输出层激活函数是 softmax，目标函数是交叉熵+大量标注数据->避免了差的局部极小值
• 正则化+dropout->改善过拟合
• 没有使用逐层预训练

自编码器的变种

• 正则自编码器：
  • 应用：使提取的特征表达符合某种性质
• 稀疏自编码器：
  • 应用：提取稀疏特征表达（假设：高维而稀疏的表达是好的）
• 去噪自编码器：
  • 应用：提取鲁棒特征表达（假设：能够对”被污染/破坏”的原始数据编码，解码，还能恢复真正的原始数据，这样的特征才是好的）
• 变分自编码器：
  • 原理：基于隐层特征表达空间 Z，通过解码层，生成样本。
  • 非监督生成模型，与对抗式生成网络 GAN 关系密切，是深度学习-概率图模型桥梁。
  • 应用：数据生成，缺失数据填补，图像超分辨率

过拟合与欠拟合

欠拟合：训练器的一般性质尚未被学习器学好（训练误差大）

解决欠拟合的思路：

• 目标：提高模型复杂度
  • 决策树：拓展分支
  • 神经网络：增加训练轮数

过拟合：学习器把训练集特点当做样本的一般特点（训练误差小，测试误差大）

解决过拟合的思路：

• 目标：降低模型的复杂度
  • 优化目标加正则项
  • 决策树：剪枝
  • 神经网络：early stop, dropout
  • 数据增广（训练集越大，越不容易过拟合）
    • 计算机视觉：图像旋转，缩放，剪切
    • 自然语言处理：同义词替换
    • 语音识别：添加随机噪声

深层网络的局部极小值产生的原因

• 深层网络的局部极小值主要是多个隐层复合导致的。
• ReLU 就是凸激活函数，但多个凸激活函数的复合也不一定是凸的。

逐层预训练真的是为了找到更好的局部极小值么？

其在一定的程序上可以帮助找到更好的局部极小值。但是，深度网络参数太多，梯度下降在非常高维空间进行，很难在所有上都是局部最小的局部极小值。大多数情况参数落在了鞍点处：某些维度上是最低点，某些维度上是最高点。

可以通过增加扰动很容易跳出鞍点的方法来摆脱鞍点。

pytorch基本操作

安装并导入pytorch库

import torch

创建一个Tensor

• ones:创建一个全为1的张量
• zeros:创建一个全为0的张量
• eye:创建一个单位矩阵
• arange:创建一个从开始值到结束值的等差数列张量
• linspace:创建一个在指定区间内的等间隔数列张量
• rand:创建一个在[0, 1)区间内均匀分布的随机数张量
• randn:创建一个标准正太分布(均值为0，标准差为1)的随机数张量
• normal:创建一个正太分布的随机数张量，可以指定均值与标准差
• uniform：创建一个均匀分布的随机数张量
• randperm：创建一个包含从0到n-1的随机排列的张量
• empty：创建一个空张量->使用该函数创建的张量是没有被初始化的，不可以直接使用

使用以上的函数创建的变量与使用tensor函数创建的变量是一个类型

创建时指定数据类型

创建时指定变量的类型：在函数的最后一行加入 dtype=torch.[类型]即可。可以使用的类型有：torch.float32, torch.float64, torch.float16, torch.uint8, torch.int8, torch.int16, torch.int32, torch.int64

m = torch.zeros(2, 3, 4, dtype=tensor.long)

利用原来的张量生成一个新的张量

创建的张量与原来张量设备属性与数据类型一致

可以使用new_*()函数来在原有的张量上生成一个新张量。通过这种方式，可以利用原有的tensor的dtype，device，的属性信息。即：数据类型与设备属性的信息一样。

创建的张量与原来张量的维度一致

可以使用*_like()函数在创建。同时，其设备属性与数据类型也会保持一致。

randn_like 函数是 PyTorch 中用于创建一个与给定张量形状相同的张量，但其元素是从标准正态分布（均值为0，标准差为1）中随机采样得到的。这个函数非常方便，尤其是在需要创建与现有张量形状相同但具有随机值的张量时。

使用方法

torch.randn_like(input, *, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format)

参数说明

• input: 需要指定形状的参考张量。
• dtype (可选): 指定输出张量的数据类型。如果不指定，则使用 input 的数据类型。
• layout (可选): 指定输出张量的布局。如果不指定，则使用 input 的布局。
• device (可选): 指定输出张量的设备（如 CPU 或 GPU）。如果不指定，则使用 input 的设备。
• requires_grad (可选): 如果设置为 True，则输出张量会记录操作以便进行自动求导。 memory_format (可选): 指定输出张量的内存格式。

完全复制一个张量

可以使用torch.clone()函数来复制一个张量。两个张量内容完全相同，但是相互不影响。

d = torch.arange(0, 10, 2)  # 创建一个从0到10（不包括10），步长为2的张量
print(d)
d1 = torch.arange(1, 10)
print(d1)
e = torch.linspace(0, 1, steps=5)  # 创建一个从0到1，包含5个等间隔数的张量
print(e)
g = torch.randn(2, 4)  # 创建一个2x4的张量，元素为标准正态分布的随机数
print(g)
i = torch.empty(2, 2).uniform_(0, 10)  # 创建一个2x2的张量，元素为[0, 1)区间内的均匀分布随机数
print(i)
j = torch.empty(2, 2)
print(j)

tx = torch.ones(2,3)
ty = tx.new_ones(5,4)
print(ty)
tz = torch.ones_like(tx)
print(tz)

tcopy = torch.clone(ty)
print(tcopy)

pytorch的操作

size函数

在pytorch中，size()函数用于获取张量的尺寸。有常见的两种用法：

1. 获取张量的整体尺寸：直接调用size函数

   m = torch.Tensor([[2, 5, 3, 7],
          [4, 2, 1, 9]])
   m.size()

2. 获取张量在特定维度上的尺寸 调用size(dim)，dim表示维度的索引，可以返回在该维度上的大小。第0维表示行数，第1维表示列数

numel()函数

该函数用于返回一个张量中的元素的数量

矩阵相乘

• 使用@来完成矩阵相乘
• 使用*来完成逐元素相乘

矩阵转置

• 使用.t()函数完成转置
• 在 PyTorch 中，transpose 函数用于交换张量的两个维度，从而实现矩阵的转置操作。具体来说，transpose 函数可以用于交换任意两个维度，而不仅仅是二维矩阵的行和列。

.t()是.transpose(0,1)的简写

矩阵拼接

• 使用.cat()函数完成拼接

m = torch.ones(2,4, dtype=torch.long)
print(m)
print(m.size(0), m.size(1), m.size(), sep=' -- ')
print(m.numel()) # 24 = 2 * 3 * 4
print(m[0][2])

# 返回第0列的所有的元素
print(m[:,0])
# 返回第1行的所有的元素
print(m[1,:])

v = torch.arange(1,5)
print(m)
print(v)

print(m@v)
print(m*v)

# 在PyTorch中，v的形状是(4,)，这意味着它是一个一维张量，包含4个元素。这个一维向量既可以解释为行向量，也可以解释为列向量，具体取决于操作的上下文。
# 进行矩阵乘法m@v时，PyTorch会自动将v解释为一个列向量（即形状为(4,1)的矩阵），因为这是符合矩阵乘法规则的解释方式。矩阵乘法要求m的列数与v的行数匹配

print(m[[0],:].size())
print(m[[0],:]@v)
print(m[0,:].size())
print(m[0,:]@v)

#m[0, :]:
#返回张量 m 的第一行。
#返回结果是一个一维张量，形状为 (4,)。

#m[[0], :]:
#返回张量 m 的第一行，但保持了二维张量的形状。
#返回结果是一个二维张量，形状为 (1, 4)。

addNum = torch.zeros(2, 4)
# 矩阵相加时，要求其形状相同
print(m + addNum)

print(m)
print(m.t())
print(m.transpose(0, 1))

# 使用transpose交换高维矩阵
highdim = torch.rand(3, 4, 2)
print(highdim)
print(highdim.transpose(1, 2))
# 第一维的2与第2给的1


# 使用matplotlib来绘图
from matplotlib import pyplot as plt
plt.hist(torch.randn(1000).numpy(), 10);

使用pytorch来构建一个线性神经网络

网络层

线性层

nn.Linear(in_features, out_features, bias=True)

in_features 是输入特征的数量，out_features 是输出特征的数量。

卷积层

nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0)

in_channels 是输入通道数，out_channels 是输出通道数，kernel_size 是卷积核大小。

循环层

nn.LSTM(input_size, hidden_size, num_layers=1)

input_size 是输入特征的数量，hidden_size 是隐藏层特征的数量，num_layers 是LSTM层的数量

激活函数

ReLU

nn.ReLU()

常用于隐藏层的激活函数，能够引入非线性。

Sigmoid

nn.Sigmoid()

将输入映射到 (0, 1) 之间，常用于二分类任务的输出层。

Tanh

nn.Tanh()

将输入映射到 (-1, 1) 之间。

Softmax

nn.Softmax(dim=x)

常用于多分类问题的输出层，将输出转换为概率分布。

损失函数

损失函数（也称为成本函数）是评估模型预测结果与真实标签之间差异的度量。通过最小化损失函数的值，可以优化模型的参数，使其预测结果更加准确。

交叉熵损失

nn.CrossEntropyLoss()

常用于多分类任务。

均方误差

nn.MSELoss()

常用于回归任务。

负对数似然损失

nn.NLLLoss()

常与 nn.LogSoftmax 一起使用。

平滑 L1 损失

nn.SmoothL1Loss()

结合了L1和L2损失的优点，适用于回归任务。

二元交叉熵损失

nn.SmoothL1Loss()

用于二分类任务，计算二元交叉熵损失。

线性网络模板

# 定义学习率与L2 正则化参数

learning_rate = 1e-3
lambda_l2 = 1e-5

# 定义模型
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    # ...
    nn.Linear(H, C),
)

# 部署模型
model.to(device)
# 选择一个损失函数
criterion = torch.nn.xxx
# 选择一个优化器
optimizer = torch.optim.xxx

#训练
for t in range(xxx):
  # 计算预测的结果
  y_pred = model(X)
  # 计算损失
  # criterion(predicted_value, real_value)
  loss = criterion(y_pred, Y)
  #其他的处理
  # 将梯度置0
  optimizer.zero_grad()
  # 反向传播优化
  loss.backward()
  # 更新全部参数
  optimizer.step()

# 训练完成

使用pytorch构建无隐层网络，单隐层网络，双隐层网络

IN:输入的维度，OT:输出的维度，H:隐层维度
上下层之间的网络的维度要对齐

无隐层网络

nn.Sequential(
    nn.Linear(IN, OT)
)

单隐层网络

nn.Sequential(
    nn.Linear(IN, H),
    nn.ReLU(),
    nn.Linear(H, OT)
)

双隐层网络

nn.Sequential(
    nn.Linear(IN, H),
    nn.ReLU(),
    nn.Linear(H, H),
    nn.ReLU(),
    nn.Linear(H, OT)
)

课后作业

代码练习

1. pytorch基本使用
2. 螺旋数据分类

文件中的重点内容均已整理到上文中。

• 使用pytorch完成矩阵计算

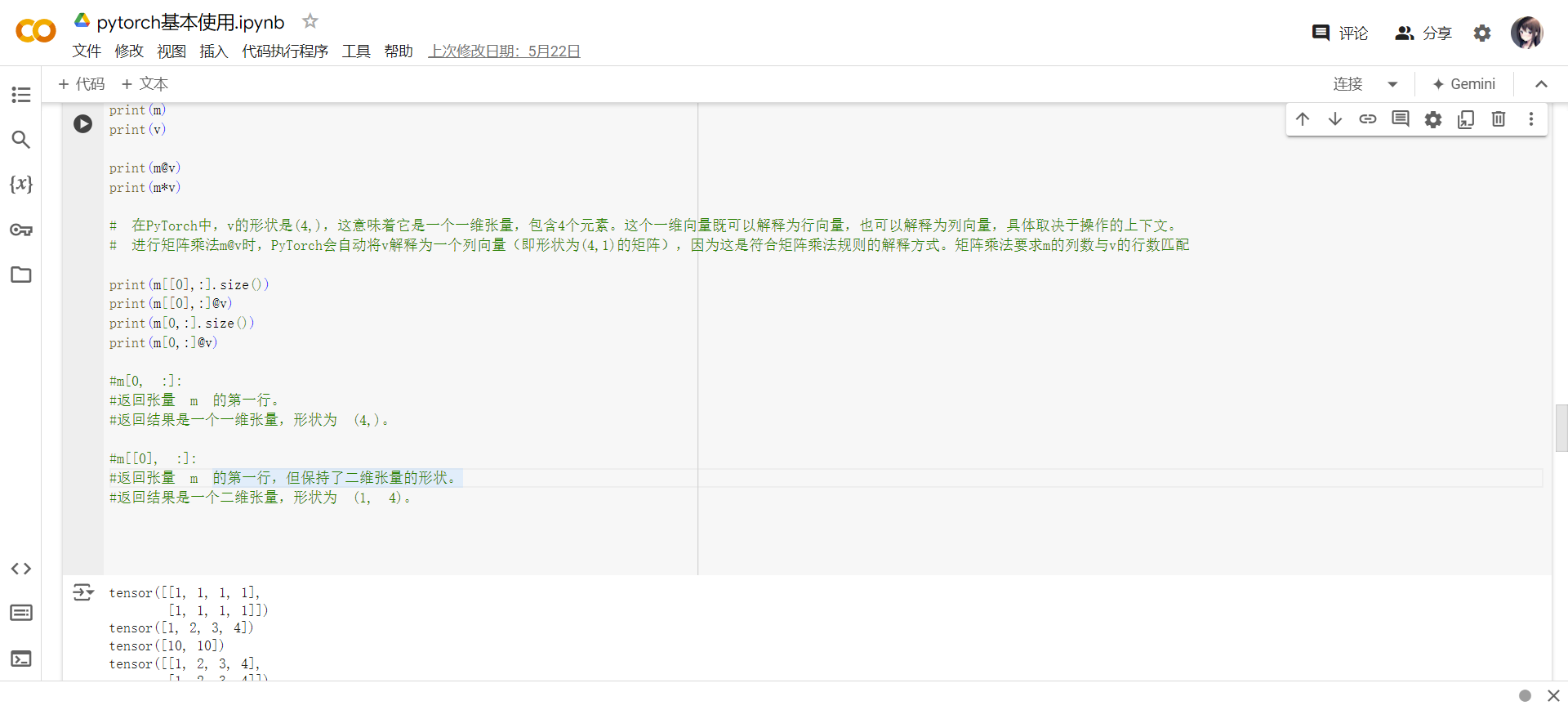
• 使用单隐层网络完成螺旋分类

当时在阅读这段代码时，我原以为它与前面的代码只有模型部分不同。后来，我对之前代码的模型部分进行了修改（在两个线性层之间加入ReLU激活函数），但发现准确度始终无法提升。对比参考代码后，我发现优化器也从 SGD 改成了 Adam。我能想到的一个可能的解释是：SGD 可能陷入了局部最优解，而使用 Adam 则有助于跳出局部最优解。

• 代码中可能存在的小问题

文件plot_lib.py中第40行代码：

zieger = plt.imread('res/ziegler.png')

该代码要求读取工作目录下res文件夹中的ziegler.png文件。

但是该文件并没有下载。所以要使用以下代码来下载文件：

!wget https://raw.githubusercontent.com/Atcold/pytorch-Deep-Learning/master/res/ziegler.png

并在工作目录下新建一个目录res，然后将下载下来的图片放到该文件夹中即可。

问题回答

AlexNet有哪些特点？为什么可以⽐LeNet取得更好的性能？

在大结构上，传承了LeNet的基本结构：卷积与池化。

其性能会更好的原因有以下三点：

1. AlexNet采用了ReLU激活函数，来代替Sigmoid函数来对输入的非线性进行优化，其计算成本更低。同时，ReLU不会在饱和区域产生梯度消失而减慢收敛速度的情况。此外，ReLU增加了矩阵的稀疏性，从而防止了过拟合。
2. AlexNet在全链接刷去采用了DropOut技术，这个技术可以让模型的泛化性更强。对消除过拟合有奇效。
3. 引入了图像增广，可以扩大数据集的规模。此外，随机改变训练样本可以降低模型对某些属性的依赖，从而提高模型的泛化能力。

激活函数有哪些作⽤？

常见的激活函数有：

• ReLU:常用于隐藏层的激活函数，能够引入非线性。
• Sigmoid:将输入映射到 (0, 1) 之间，常用于二分类任务的输出层。
• Tanh:将输入映射到 (-1, 1) 之间。
• Softmax:常用于多分类问题的输出层，将输出转换为概率分布。

梯度消失现象是什么？

当神经网络在进行训练时，输入数据经过前馈传播得出结果，然后优化器则会根据误差来调整模型中的参数。调整的顺序则是从最后一层向第一层调整（反向传播）。

神经网络使用梯度来完成对误差的传递。但是对于某些特定的激活函数，比如sigmoid，当输入的值较大时，其导数则可能趋近于0。此时，上一层接收到的梯度就变得很小，等上一层调整完以后还要再次传递到上上一层，此时，梯度的值可能也会趋近于0。上上一层收到趋近于0的梯度则对其调整几乎没有参考意义。

因此，在训练后，底层的网络层调整的很好，可是顶层却几乎没有被调整（收到的梯度很小，无法受到有效的调整）。这个现象就是梯度消失。

神经⽹络是更宽好还是更深好？

• 在神经元总数相当的情况下，增加网络深度可以比增加宽度带来更强的网络表示能力：产生更多的线性区域

• 深度和宽度对函数复杂度的贡献是不同的，深度的贡献是指数增长的，而宽度的贡献是线性的。

为什么要使⽤Softmax?

在多分类问题，softmax函数可以将模型的输出转换为每个类的概率，这样可以很方便的确定输入的数据属于哪个类别。

SGD 和 Adam 哪个更有效？

SGD与Adam各有各的优点，通常情况下Adam有更好的表现。

疑问

1. 既然自编码器的目标是将隐层可以最大程度的表示输入，那么为什么不直接取消该层，直接使用输入的数据？

自编码器可以提取输入数据的整体的结构，如果目标模型不需要关注细节，只需要关注整体结构，则可以使用自编码器。此外，自编码器还可以完成图像的修复，比如去噪，去雨，去雾，超分辨率等。

2. 不同的激活函数对应不同的效果，是不是在写代码的时候直接无脑选择当前最先进的激活函数？

激活函数一般使用ReLU就已经可以获得足够的效果。

3. 像受限玻耳兹曼机的条件概率建模，要不要学习这些公式。

不用学习公式了，RBM已经淘汰了，不需要看了。