FourierMamba- Fourier Learning Integration with State Space Models for Image Deraining

发表于 2024-07-02 更新于 2024-07-04 分类于论文阅读

论文地址：arxiv

摘要

背景

图像去雨的目的是从雨天的图像中去除雨条纹并恢复清晰的背景。

当前研究的不足点

现在有使用傅里叶变换来进行图像去雨，但是基于此的方法通常无法充分复用图像中低频与高频的相关性，从而限制了它们的效果。

创新点

通过将 mamba 技术与傅里叶空间相结合，通过关联不同频率，从而进行图像的雨效果。

正文

傅里叶变换的有效性

傅里叶变换可以在一定程序上分离图像劣化和内容成分
傅里叶有全局性，傅里叶空间中的每个像素都与所有空间像素相关

使用 Mamba 的原因

Mamba 的选择性方法可以明确构建图像块或像素之间的相关性。Mamba 在空间和时间等各个领域都有效果并且效率不差。

创建点核心

提出了新的框架，叫 FourierMamba，它在傅时叶域中使用 Mamba 进行图像去雨。从空间与通道的维度设计了傅里叶域中的 Mamba 框架。同时考虑到傅时叶域中频率顺序的独特的排列，FourierMamba 的核心在于对不同频率的扫描编码，其中低-高频顺序在空间轴上未排列而在通道轴上排列。

在傅里叶空间的空间维度中，低频与高频号同心圆排列，低频位于中心附近，高频位于外围。而使用 JPEG 的压缩之字形编码，可以将低频系数置于数组的前端，而高频系数位于末尾。因此将其引入来扫描空间维度中的频率。同时，由于傅里叶空间中频率顺序的对称性，通过类似环绕的方式实现，来匹配傅里叶空间中对称频率顺序。通过这种方式有序的关联了频率之间的连接。

在傅里叶空间的通道维度中，频率顺序沿轴排列，从中间的低频到两侧的高频。

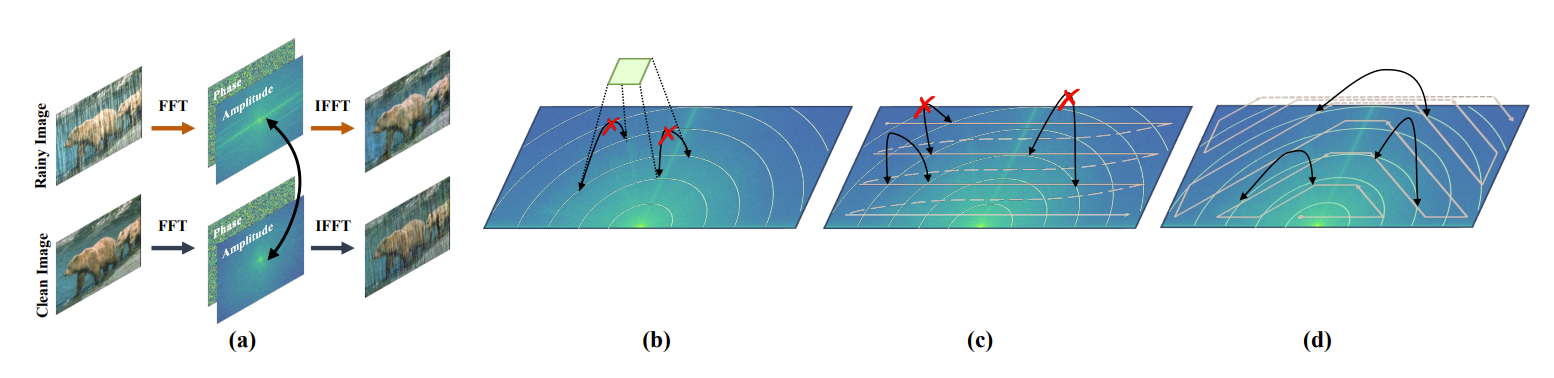
b 为不使用之字形扫描法，c 为使用普通的之字形扫描法，d 为文中所使用的扫描法。

贡献

提出了 FourierMamba，将傅里叶先驱与状态空间模型结合起来，以关联傅里叶空间中不同频率，从而增强图像去雨的效果
为了在傅里叶空间的空间维度中从低频到高频重新排列顺序，提出了一种基于之字形编码的扫描方法来有序的关联不同频率
基于通道维度的傅里叶变换，利用 Mamba 在通道上进行扫描并关联不同频率，来改善通道信息表示。

傅里叶变换

傅里叶变换是一种广泛用于分析图像频率内容的技术。对于具有多个颜色通道的图像，傅里叶变换分别应用于每个通道。傅里叶变换在全局建模中展示了其有效性。这种变换将信号转换到一个由全局统计特性描述的域中。由于其在全局建模中的有效性，傅里叶变换已被引入低级视觉任务。

本论文在傅里叶域中引入了一种渐进扫描策略，增强了全局建模能力，同时解决了视觉 Mamba 的方向敏感性问题。

对于图像 $X$，傅里叶变换 $F$ 将其转换为伺机而动里叶空间的复数分量 $F(x)$，其表达式为：
$$
F(x)(u, v) = \frac{1}{\sqrt{HW}}\sum^{H-1}{h=0}\sum{w=0}^{W-1}x(h, w)e^{-j2\pi(\frac{h}{H})u+\frac{w}{W}v}
$$
其中，$u$ 与 $v$ 表示傅里叶空间的坐标。$F^{-1}(x)$ 定义了相应的逆傅里叶变换。傅里叶变换与其逆变换可以通过 FFT/IFFT 算法高效实现。幅度分量 $A(x)(u, v)$ 与相位分量 $P(x)(u,v)$ 表达为：
$$
A(x)(u,v)=\sqrt{R^2(x)(u,v)+I^2(x)(u,v)}
$$
$$
P(x)(u,v) = arctan(\frac{I(x)(u,v)}{R(x)(u,v)})
$$
其中 $R(x)(u,v)$ 和 $I(x)(u,v)$ 分别表示实部和虚部。傅里叶变换及其逆变换分别应用于特征图的每个通道。

通道维度傅里叶变换

通过对每个空间位置的通道维度单独应用傅里叶变换来引入通道维度傅里叶变换。

对于 x 中的每个位置（h, w）表示为 $x(h, w, 0 : C-1)$ 并简写为 $y(0:C-1)$，傅里叶变换 $F(*)$ 将其转换为傅里叶空间的复数分量 $F(y)$，其表达式为：
$$
F(y(0:C-1))(z)=\frac{1}{C}\sum_{c=0}^{C-1}y(c)e^{-j2\pi\frac{c}{C}z}
$$
同样，$F(y(0:C-1))(z)$ 的幅度分量 $A(y(0:C-1))(z)$ 和相位分量 $P(y(0:C-1))(z)$ 表达式为：
$$
A(y(0:C-1))(z) = \sqrt{R^2(y(0:C-1))(z)+I^2(y(0:C-1))(z)}
$$
$$
P(y(0:C-1))(z) = arctan(\frac{I(y(0:C-1))(z)}{R(y(0:C-1))(z)})
$$
这些操作可以应用于通过池化操作到的全局向量。这样，$A(z)$ 与 $P(z)$ 分别表示不同通道频率的幅度和方向变化。这两个度量概括了与通道信息相关的全局统计数据。

傅里叶空间扫描

选择扫描机制（S 6）因为其独特的因果方式来处理数据，所以无法直接应用于扫描图像块。还会导致”方向敏感性”问题。而对于图像修复来说，傅里叶宰及其相关先验知识至关重要。因此，要设计在傅里叶空间内解决”方向敏感性”问题。

通过在空间与通道维度定制傅里叶扫描策略。在空间维度上，傅里叶空间中的每个像素点包含全局信息，其频率分布在同心圆中。而基于空间排列的扫描方法会破坏频域中的高低频关系，从而阻碍图像退货信息的建模。因此设计了一种傅里叶空间中的扫描方式：

直观方法：计算频谱中每个点到中心点的欧几里得距离，但这种方法计算开销较大。
Zigzag 编码方法：受 JPEG 压缩中的 Zigzag 编码启发，提出了一种扫描幅度和相位光谱的方法，避免了对称性破坏的问题。
而 Zigzag 有两种扫描方式：
双向 Zigzag：从频谱一侧的最高频率顶点开始，以 Zigzag 模式向中心前进，再前进到另一侧的最高频率。该扫描方法不仅建模了高频和低频之间的关联，还考虑了傅里叶频谱的周期性。
渐进 Zigzag：基于 Zigzag 扫描建立的低到高频序列，进行从低到高频率的扫描。这种方法的动机是神经网络在提取图像特征时倾向于首先学习低频信息。

以上两种扫描方式的图像化表示如下：

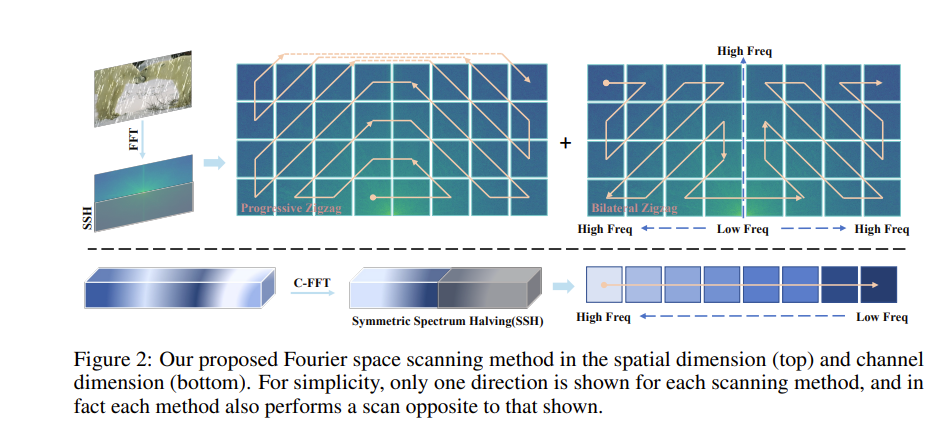
傅里叶通道维度的扫描

对于通道维度的傅里叶空间，由于它是按低到高频率顺序排列的一维序列，我们直接对其进行一维扫描。同样，由于傅里叶变换的对称性，我们只扫描一半并推导出另一半。通过在空间和通道维度的傅里叶空间扫描，我们可以有序地关联频率之间的连接，从而充分利用频率信息来提高去雨效果。

FourierMamba

总体结构

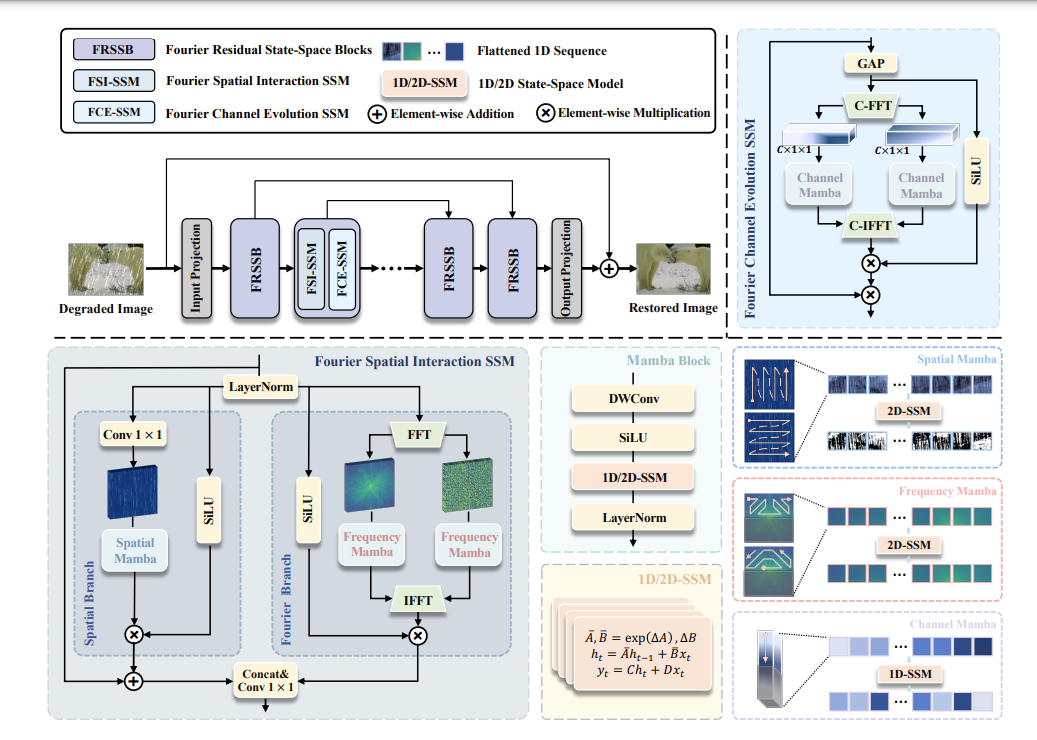
首先使用 3*3 的卷积层生成维度为 $HWC$ 的浅层特征，其中 $H$ 与 $W$ 分别表示调度与宽度，$C$ 表示通道数。随后，使用和多尺度 $U_{Net}$ 架构来获取深层特征。该阶段由一组堆叠的 Fourier 状态组（fourier residual state-space group）组成，每组包含若干 Fourier 状态空间块（FRSSB）。FRSSB 融合了两个核心设计：Fourier 空间交互 SSM 块与 Fourier 通道演化 SSM 块。它们分别从这空间与通道维度关联傅里叶域信息，来充分利用频率信息。

Fourier 空间交互 SSM

该模块处理如下：用 LayerNorm 将输入特征 $F_{in}$ 转换为 $F_{l}$，为了促进空间与频率信息之间的交互，FSI-SSM 用傅里叶分支和空间分支协同处理 $F_{in}$。

傅里叶分支

通过快速傅里叶变换，$F_{l}$ 被转换为傅里叶谱，随后分解为幅度谱 $A(F_{l})$ 与相位谱 $P(F_{l})$。幅度谱与相位谱分别使用渐进频率扫描方法处理，来得到 $A’(F_{l})$ 与 $P’(F_{l})$。

序列变换采用以下操作序列：DWConv -> SiLU -> SSM -> LayerNorm。然后对处理后的谱进行逆傅里叶亦称，并将其与 SiLU 的输出相乘。
$$
F_{f}=(F^{-1}(A’(F_{l}), P’(F_{l}))) \odot SiLU(F_{l})
$$
$F_{f}$ 为该傅里叶分支的输出，$\odot$ 为 Hadamard 积

空间分支

在空间域中，会将输入特征 $F_{l}$ 送往两个并行子分支。一个子分支使用 SiLU 函数激活特征。另一个子分支在 1*1 卷积后对特征执行空间 Mamba。空间 Mamba 采用与上术频率分支相同的操作序列，但在 SSM 中的扫描使用二维选择性扫描模块。最后两个子分支的输出进行像素级相乘来获得输出 $F_{s}$

之后使用连接将空间输出添加到 $F_{in}$。空间分支在空间域中捕获全局特征，补充了傅里叶分支在频率域中捕获的频率相关性，从而有得于图像去雨的性能。最后，将空间与频率分支的输出进行拼接，并使用 1*1 卷积融合空间与频率信息。

傅里叶通道演化 SSM

由于在通道维度傅里叶变换后，每个通道都包含了所有通道的信息，在傅里叶域中进行通道交互，可以有效的关联不同频率的通道。傅里叶通道演化 SSM（FCS_SSM）由三个连续部分组成：沿通道维度应用傅里叶变换以获得通道级的傅里叶域特征，扫描其幅度和相位，然后恢复到空间域。

对于输入特征 $F_{r}$，先对其进行全局平均池化
$$
F_g = \frac{1}{H_r W_r} \sum_{h=0}^{H_r-1} \sum_{w=0}^{W_r-1} F_g(h, w)
$$
而 $F_{g}$ 对应于 $F_r$ 的幅度谱的中心点，可以有效的封装了特征的全局信息。然后使用通道维度傅里叶变换对 $F_{g}$ 进行变换来得到 $F(F_{g})(z)$。基于此，使用对应的公式获得幅度分量 $A(F_g)(z)$ 与相位分量 $P(F_g)(z)$。由于幅度谱与相位谱有明显的信息意义，所以对这两个分量进行 Mamba 扫描
$$
A(F_g)(z)’ = \text{ChaScan}(A(F_g)(z)), \quad P(F_g)(z)’ = \text{ChaScan}(P(F_g)(z))

$$
其中 ChaScan 是一个使用以下操作序列的一维序列变换：DW Conv → SiLU → SSM → LayerNorm。在 Mamba 关联了通道维度中的不同频率之后，我们对其进行逆傅里叶变换，并将结果与 SiLU 激活后的通道特征相乘。
$$
F_a = (F^{-1}(A(F_g)(z)’, P(F_g)(z)’)) \odot \text{SiLU}(F_g)
$$
$F_{a}$ 是在关联了不同频率后的通道特征。最后，将其与空间特征以注意力的形式相乘来获得输出 $F_{c}$
$$
F_c=F_a \odot F_r
$$

优化

在空间域与频域都加了约束，在空间域中，利用最终输出 $Y_{out}$ 与真实值 $Y_{gt}$ 之间的 L 1 损失。在频域中，基于傅里叶亦称应用 L 1 损失。整体的损失函数如下：
$$ L_{\text{total}} = || Y_{\text{out}} - Y_{\text{gt}} ||1 + \lambda || F(Y{out}) - F(Y_{\text{gt}}) ||_1 $$

模型的效果

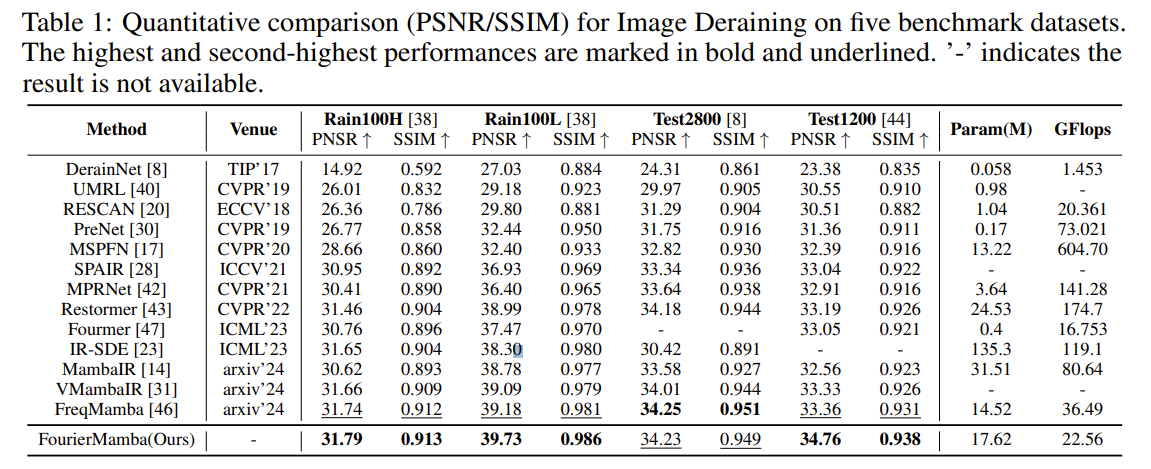
可以看到该方法在所有数据集上都实现了最高的 PSNR 和 SSIM。

通过比较在 Rain 100 H 数据集中具有高难度的退化图像的视觉质量。可以发现在面对复杂或极其严重的条纹时，该方法都可以取得优异的结果：

消融实验

Fourier 空间交互 SSM（FSI-SSM）和 Fourier 通道演化 SSM（FCI-SSM）

将 FSI-SSM 与 FCE_SSM 中和 mamba 扫描替换为 1*1 卷积，分别称为 w/o FSI-SSM和w/o FCE-SSM。从以下表中可以看出，1*1 卷积无法建模不同频率的依赖性，其性能比原设计在通道维度上与空间维度上都要差。

Fourier 先验

分别不在空间维度和通道维度使用 Fourier 变换，而是直接进行 mamba 扫描，分别称为无空间维度 Fourier（w/o SDF）和无通道维度 Fourier（w/o CDF）。可以从上表中看出，在生动了空间维度与通道维度的先验后，性能显著下降。

Fourier 空间中的扫描方法

比较了几种空间维度 Fourier 空间的扫描方法，计算量相同。可以从下表中看出，本文提出的扫描方法要优于传统的二维扫描方法。同时，由于互补性，这两种方法的结合也可以进一步的提高性能。