A Spatiotemporal Multiscale Deep Learning Model for Subseasonal Prediction of Arctic Sea Ice
论文地址:researchgate
摘要
基于物理的动力学模型可以成功的预测短期海冰趋势,但是在较短时间内提供可靠的次季节海冰预测方面存在困难,并且缺乏足够的灵活性来提供实时、准实时预测。
作者提出了一个纯粹基于数据驱动的北极海冰预测系统,叫 IceFormer。它通过高质量的北极再分析数据和遥感观测数据进行训练。
通过实验可以证明:在北极海冰的级多变量预测方面取得了进展。在遥感数据的驱动下,其预测性能远优于传统基线模型和机器学习模型。经过比较,从 5 月到 11 月,IceFormer 的 SIC 预测性能优于耦合集合数值预报模型(SEAS 5)
正文
虽然 SICNet 结合了多个观测数据,但是由于不同的来源的数据质量差异会很大,所以作者只使用海冰变量来驱动模型,这可以有效降低模型的复杂性与不确定性,同时也方便开展业务预测工作。
所以作者提出了 IceFormer,这是一种纯数据驱动的模型框架,可以用来预测泛北极地区每日海冰浓度(SIC)和海冰厚度(SIT)。IceFormer 是一个基于先驱模式(PP)和网络推理(NI)的通用浓度学习模型框架。其核心设计理念是”基于对已知的充分理解来预测未知”。
北极海冰的多变量正交模式用于表示海冰多尺度演变的知识,这可以在神经网络推理之前最大化地捕获已知信息。NI的核心是基于多相关机制的预测模型。它不仅考虑了北极海冰的时空依赖性和变量依赖性,还提高了北极海冰亚季节预测的可解释性。更重要的是,IceFormer 可以以端到端的方式实现时空多尺度像素级任务,这比现有的DL模型提供了更轻量的方法。
NI 部分被设计成一个编码器-解码器结构。将每个正交模式的多尺度时间编码和贡献编码集成到 IceFormer 中,这有助于我们的模型准确捕捉时空依赖性并提高可解释性。SIC和SIT被用作 IceFormer 的唯一输入数据。
模型的材料
研究区域与变量
研究区域(图1)为泛北极地区(180°E至180°W,45°N至90°N),覆盖了北极海冰演变和观测的核心区域。
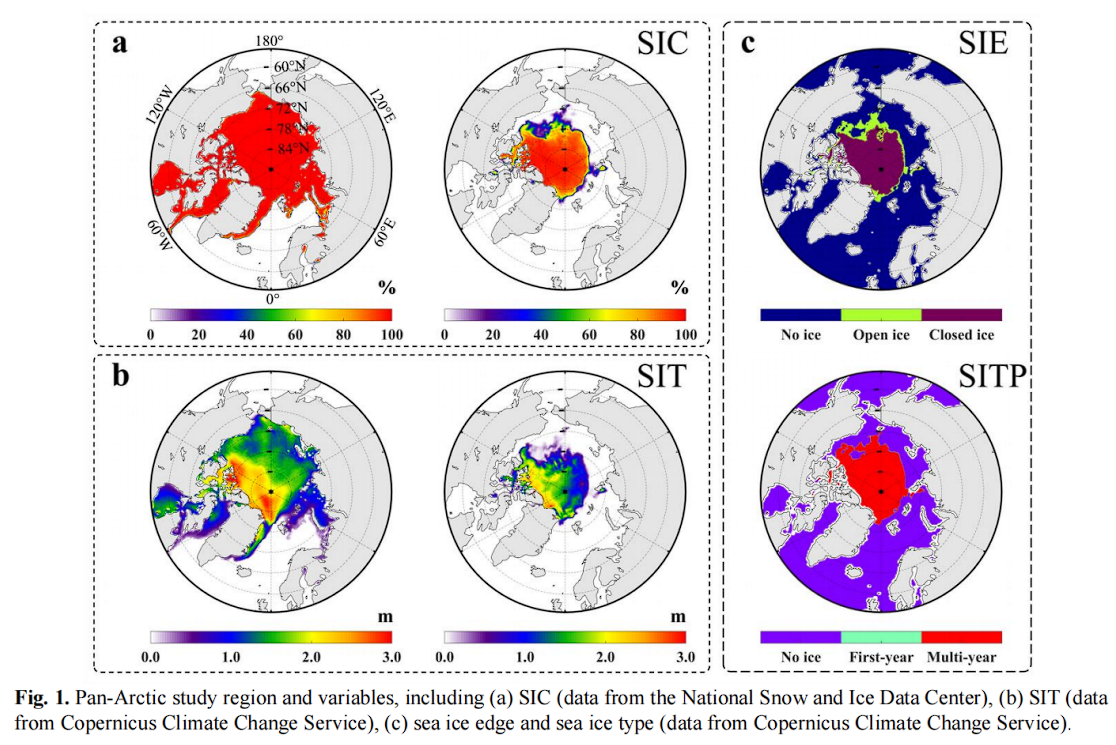
- SIC 定义为海冰覆盖面积与总海域面积的比值,是描述海冰水平分布的重要变量。
- SIT是描述海冰垂直分布特征的核心变量,其重要性与海冰浓度相当。
数据
作者考虑了 SIC 与 SIT 的多源数据(遥感观测和再分析)作为原始数据集。同时,作者还设计了从再分析数据到遥感数据的迁移学习过程。其中,再分析仅用作模型训练的扩展数据,而遥感观测则用作模型校准的驱动数据。
SIC 的数据来自:国家雪冰数据中心(NSIDC)
SIT 的数据来自:哥白尼气候变化服务(C3S)
迁移学习的再分析数据:北极监测和预报中心(ARC-MFC)提供
作者使用 PIOMAS 来作为评估 SIT 的基准,使用 SEAS 5 作为评估 SIC 的基准
模型架构
在构建 IceFormer 和进行训练之前,会先对原始的遥感数据进行预处理,并通过插值方法将具有非均匀时空分辨率的数据(图 2)重新网格化为统一的数据(图 3)。如下图所示:
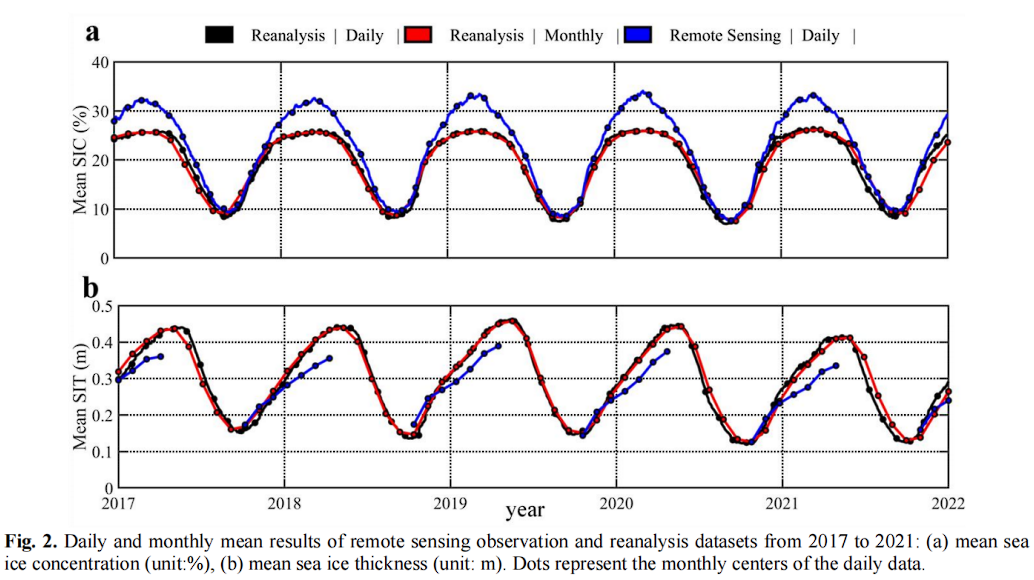
基于多变量经验正交函数理论,设计了一种算法来提取海冰浓度(SIC)与海冰厚度(SIT)的同时演化先验模式。基于每日的 SIC 和 SIT,作者开发了一个深度学习建模框架,这个框架有三个核心组件,信息嵌入,编码器,解码器。通过将 iceFormer 预测系统设计为化组合,集成了先验模型模块,映射模块,预测模块和重建模块,形成了一个标准的工作流程。
IceFormer 首先用高质量的再分析数据进行预训练,并通过遥感数据进行微调(见III-E节),以减少使用遥感观测进行 SIC 和 SIT 预测时的偏差。
时空重新网格化处理
由于 SIT 数据无法达到与 SIC 数据相同的时空分辨率,为了实现每日 SIC 和 SIT 的联合预测并确保评估过程的合理性,需要调整 SIC 和 SIT 的数据。
作者将 1991 到 2016 年的再分析数据和遥感数据用于预处理与微调,而 2017 到 2021 的遥感数据用于测试。作者对训练数据和测试数据进行时空插值。
由于 SIC 的已经满足要求,所以,只插值 SIT 数据。数据集由此制作完成。
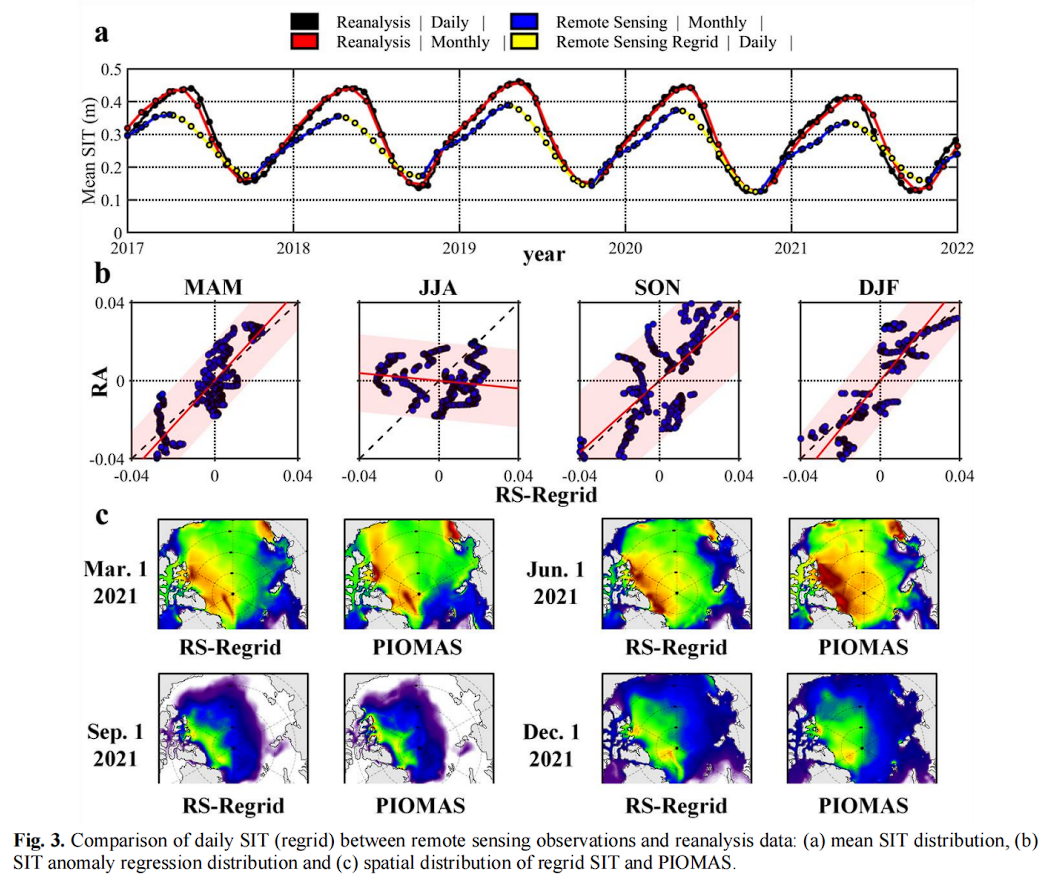
从图 3 可以看到,重新网格化的 SIT 数据与遥感观测一致。同时,季节性的 SIT 周期波动也和再分析数据相似(图 3 a)。从图 3 b 可以看到,网格化的 SIT 在三季 MAM、SON 和 DJF 中的异常值与再分析数据正相关,但在 JJA 中呈现负相关。从图 3 c 中可以看出,重新网格化的 SIT 与 PIOMAS 的每日 SIT 具有相对一致的空间形态,但仍存在明显差异。
时空序列分解
经验正交函数(EOF)是地球科学领域常用的统计分析方法,可用于分析时空分布特征。多变量经验正交函数(MV-EOF)和经典 EOF 的计算步骤基本相同,不同之处在于 MV-EOF 在构建初始异常矩阵时需要按行连接多个变量。
从公式 1 中可以看到,$X^n_{SIC}$ 表示第 n 天的 SIC 样本。样本矩阵的维度是 $2m*N$,$m$ 是每个变量的空间维度,$N$ 是变量的时间维度。
$$
\mathbf{X}{2m \times N} = \left( \begin{array}{ccc}
X^{1}{SIC} & \cdots & X^{n}{SIC} & \cdots & X^{N}{SIC} \
X^{1}{SIT} & \cdots & X^{n}{SIC} & \cdots & X^{N}{SIT} \
\end{array} \right)
$$
在进行 MV-EOF 分解之前,会扣除 $SIC$ 和 $SIT$ 的气候状态,并进一步标准化异常矩阵来获得标准化异常矩阵 $X{MN}$。其中,$M$ 是 SIC 与 SIT 的公共空间点的数据 $M=2m$,$N$ 是时间长度,然后可以计算矩阵 $X_{MN}$ 的协方差矩阵 $C_{MM}$:
$$
C_{MM}=\frac{1}{N}X_{MN}M^T_{MN}
$$
$C_{MM}$ 的特征值 $\mathbf{\Lambda}{M \times M}$ 和特征向量 $\mathbf{V}{M \times M}$ 可以表示为
$$
\mathbf{C}{M \times M} \times \mathbf{V}{M \times M} = \mathbf{V}{M \times M} \times \mathbf{\Lambda}{M \times M}
$$
$$
\mathbf{\Lambda}{M \times M} = \operatorname{diag}(\lambda_1, \ldots, \lambda_M)
$$
其中,特征值按降序排列,每个非零特征值对应于特征向量的一列,也称为空间模式。将空间模式投影到矩阵 $X{MN}$ 上可以获得与特征向量对应的主成分:
$$
PC_{MN}= V^T_{MM}X_{MN}
$$
$PC_{MN}$ 中每年的数据表示特征向量中系列对应的 PCs。
预测模块(PM)设计
预测模块专为高维相空间中的海冰演化设计。通过 PM 捕捉海冰覆盖率(SIC)和海冰厚度(SIT)的联合演化是基本需求。因此,PM 的结构设计需要采用可以推断 SIC 和 SIT 在相空间中的相关性及其多交互的结构单元。
PM 的结构如图 4 a 所示,包含三个核心单元:嵌入层,编码器和解码器。
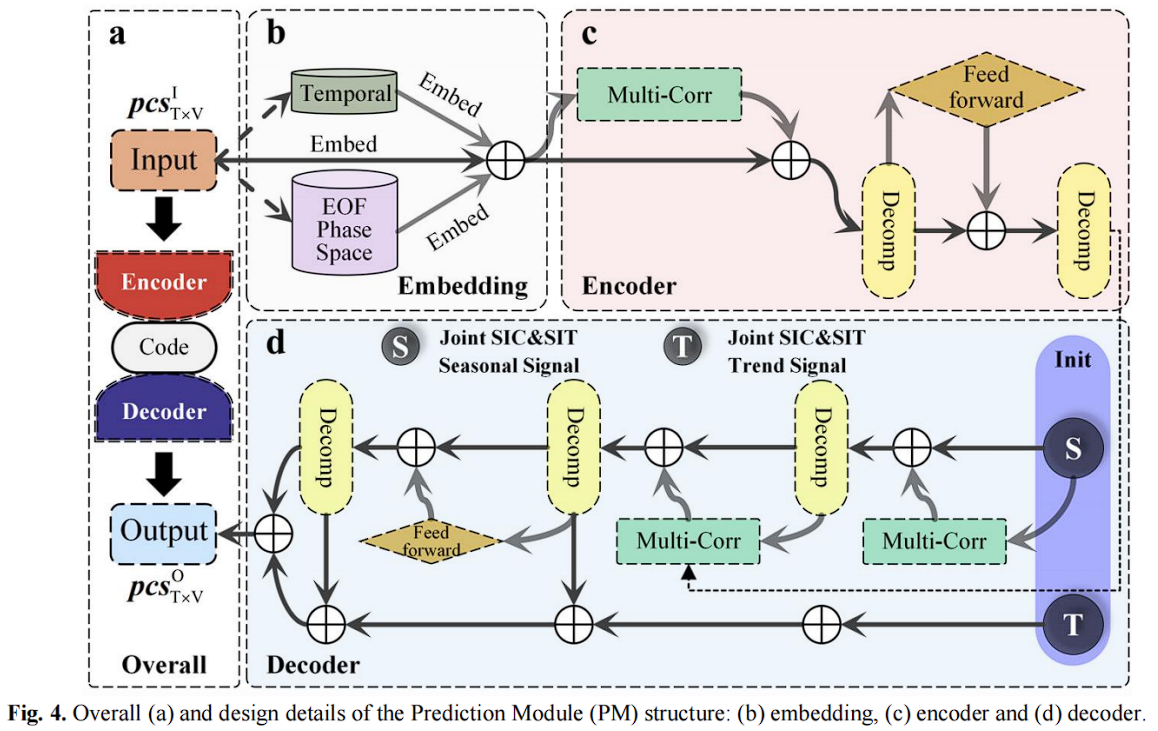
作者使用三种核心组件:前馈网络,多相关机制和分解模块。多相关性机制用于推断 EOF 空间中的 SIC 和 SIT 的自相关和交叉相关性,而分解模块用于捕捉海冰的多尺度信息。
由于 SIC 和 SIT 的联合成分(PC)不可以直接使用地理坐标进行空间标注,所以作者首先重新设计了嵌入层。SIC 与 SIT 的联合成分构成了高维的 EOF 相空间维度 $X \in \mathbb{R}^{NS*TI}$,$NS$ 是 EOF 相空间的维度,$TI$ 是输入的时间维度。EOF 相空间中的每个点都代表两个海冰变量的联合演化。
从图 4 b 中可以看到,PM 的嵌入层对 EOF 相空间,时间和联合 PC 的信息分别进行嵌入映射。嵌入层由全连接层组成。同时,嵌入层不包含激活函数与偏差信息。
EOF 相空间的每个维度中的权重信息 $X \in \mathbb{R}^{NS \times 3}$ 都被嵌入了,包括个EOF模式的方差贡献、累积方差贡献和特征值。时间信息的编码包括每个时间点的年、月和日。
$$
X_{en} = Embed_{data}(X)+Embed_{ps}(X_{ps})+Embed_{time}(X_{time})
$$
其中,$X_{en} \in R^{NSTID_{model}}$ 是编码器的嵌入输入,$D_{model}$ 是隐藏变量的通道数。相同的嵌入方式也用于解码器的输入准备。
编码过程(图 4 c)从历史观测中学习联合 PC 信息的表示,并将其输入解码器。PM 的编码器交替应用 MC 和 FF 层,来捕捉时空相关性。这个过程可以用以下来表示:
$$
\begin{cases}
\widehat{X}{en}^{i-1} = \text{MC}(X{en}^{i-1}) \
X_{en}^{i} = \text{FF}(\widehat{X}_{en}^{i-1})
\end{cases}
\quad i = 1, 2, \ldots, \text{Ens}
$$
$i$ 是编码层的编号,$X_{\text{Ens}} \in \mathbb{R}^{NS \times T \times D}$ 是从第 $i$ 个编码层中提取的演化信息。
解码器的输入是 $X_{season},X_{trend} \in \mathbb{R}^{NS \times (\frac{TI}{3}+TO)}$,分别表示未来的广义平稳季节性部分和非平稳趋势部分,包括长度为 $TI/3$ 的近历史观测和长度为 $TO$ 的未来预测占位符作为初始化。这些初始化将基于编码器中学习的时空信息在解码器中进行细化,过程为:
$$
\begin{cases}
\widehat{X}{de}^{j,1} = \text{MC}(X{de}^{j-1}) \
\widehat{X}{de}^{j,2} = \text{MC}(X{de}^{j,1}, X_{en}^{\text{Ens}}) \
X_{de}^{j} = \text{FF}(\widehat{X}{de}^{j,2})
\end{cases}
\quad j = 1, 2, \ldots, \text{Des}
$$
$j$ 是解码层的编号,$X{\text{season}}$ 和 $X_{\text{trend}}$ 被输入 PM 的解码器进行处理。最后,预测结果表示为多项式的形式。
分解模块基于沿时间维度的移动平均,可以将序列分解为具有广义平稳性和非平稳趋势的季节性部分。多相关性机制用于从分散的局部观测中发现复杂的时空相关性,以同时预测海冰。总体来说,PM在编码器和解码器内部嵌套了多个分解模块和多相关性机制,以实现海冰的时空多尺度预测。
模型的工作流程
作者建立了一个预测模块为核心的标准化工作流程。采用模块化设计,集成了四个模块:先验模式模块(Prior Patterns Module,PPM),映射模块(Mapping Module,MM),预测模块(Prediction Module,PM)和重建模块(Reconstruction Module,RM)。
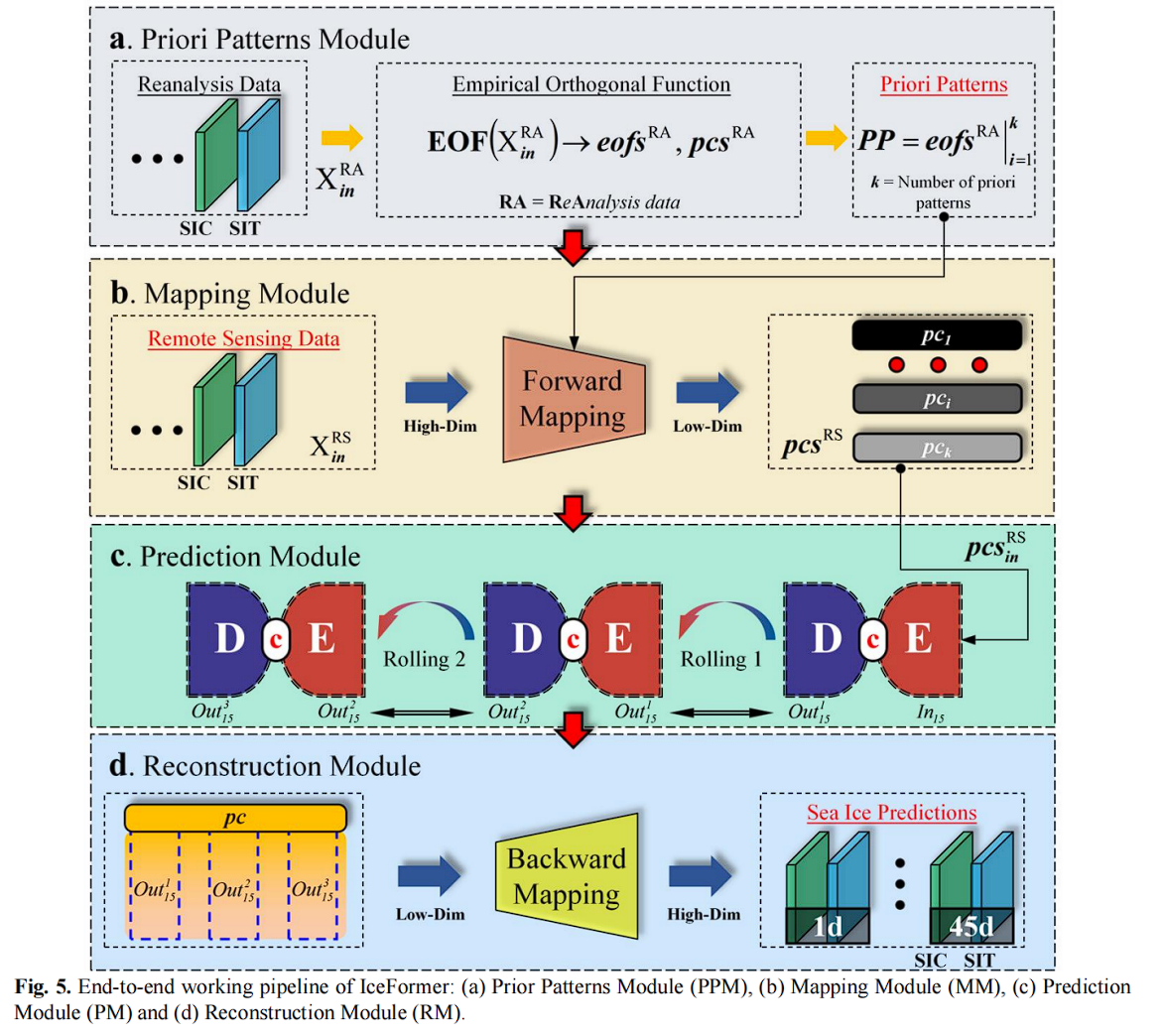
先验模式模块
图 5 a
用于提取 SIC 和 SIT 的同时演化模式,这是 EOF 分解计算过程的模块化实现。
映射模块
图 5 b
该模块在完成 PPM 的冷启动和 IceFormer 的预训练后执行。在 IceFormer 的二次训练之前,采用 1991 至 2016 年的遥感数据和 PPM 中保留的空间模式作为输入,并将观测数据投影到 EOF 空间,其中的联合PC用于IceFormer的微调。
预测模块
图 5 c
此模块是IceFormer的核心,采用编码-解码机制进行联合PC预测。该部分总共运行3次,第一次为直接预测阶段,使用15天的联合PC预测接下来的15天。最后两次为滚动预测阶段,使用前一步中预测的联合PC作为输入。最终,PM获得未来45天的联合PC。
重建模块
图 5 d
此模块是联合PC的反向映射,利用PPM保留的空间模式和PM预测的45天联合PC重建未来每日的SIC和SIT。
模型评估
作者使用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、空间异常相关系数(SACC)、二值准确率(BACC)和决定系数(R2)作为评价指标。
RMSE、MAPE和MAE是通用的误差评估指标,可以直接反映预测结果与观测结果之间的相对或绝对误差。SACC和R2从相关性的角度进行衡量,可以更清晰地反映演变趋势的相似性与差异。BACC源于综合冰缘误差(IIEE),它通过判断SIC大于15%(取值1)或不大于15%(取值0)的二值海冰面积计算得出。IIEE定义为所有SIE被高估或低估区域的总和。
总体评估
IceFormer 的训练过程大约需要 75 分钟,其核心是因为提取了海冰演变的大规模信息和主要模式,使得原本高维的地理空间映射到了低维的相空间。大规模信息和主要模式在普通 CPU 上需要运行 3 天左右,但是一但提取成功,就可以保存成为固定的文件,无需重复的计算。在这以后,IceFormer 的时间消耗则会主要集中在模型的迭代训练的部分。
其平均 SACC 和 RMSE 如图 6 所示:
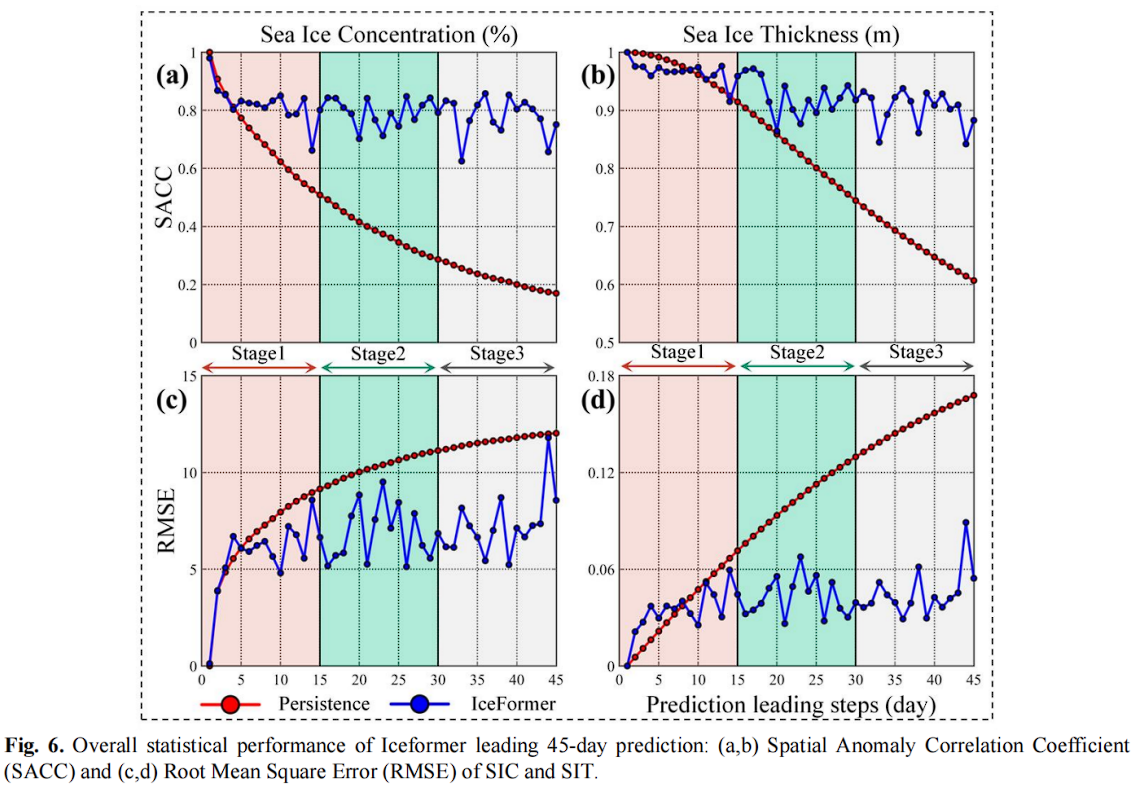
如图6所示,与基线模型相比,IceFormer在45天的海冰预测中表现远优于持续预测,这得益于IceFormer混合预测方案的设计。
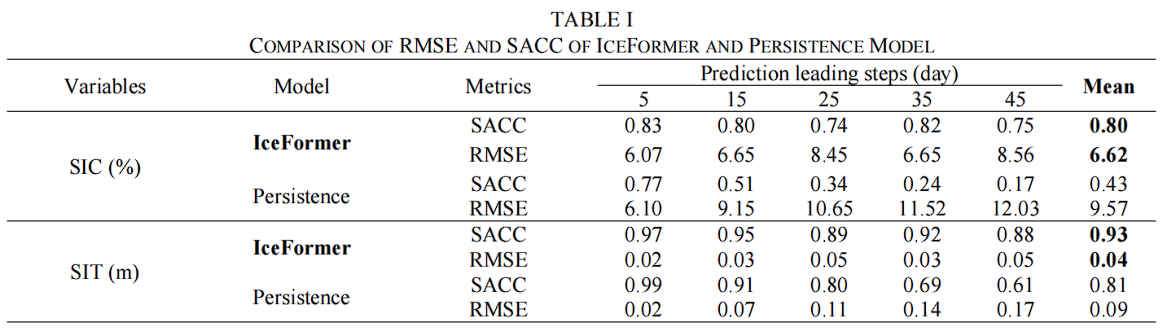
如表I所示,SIC和SIT的平均RMSE分别为6.62%和0.04米,综合SACC分别为0.80和0.93
作者还展示了SIC和SIT的RMSE在时间和空间上的分布,如图7(a)-(d)所示,并重点展示了IceFormer在融冰季节的表现。
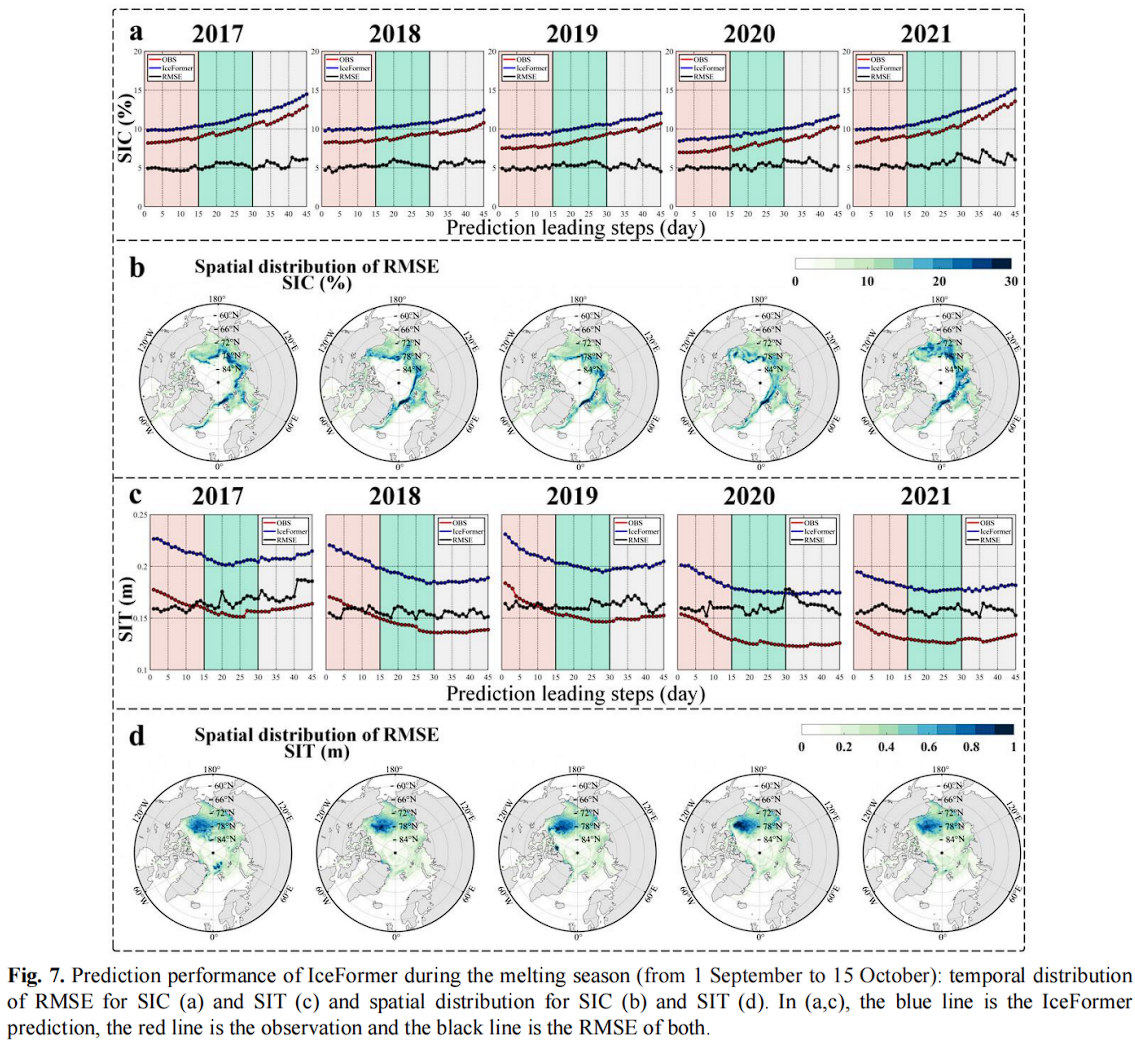
如图7(a)所示,SIC的预测与遥感观测总体趋势一致。如图7(c)所示,SIT的短期融化趋势也被准确捕捉到。
通过对每个非陆地区网格点的时间平均,得到整体RMSE的空间分布。RMSE的空间分布更直接地显示在图7(b)和图7(d)中。
如图7(b)所示,SIC在北极大部分地区的空间RMSE小于10%。主要误差分布在融冰季节的海冰覆盖边缘区域。从图7(d)可以看出,SIT的主要误差区域也是边缘区域。
使用 RS 和 PIOMAS 进行验证
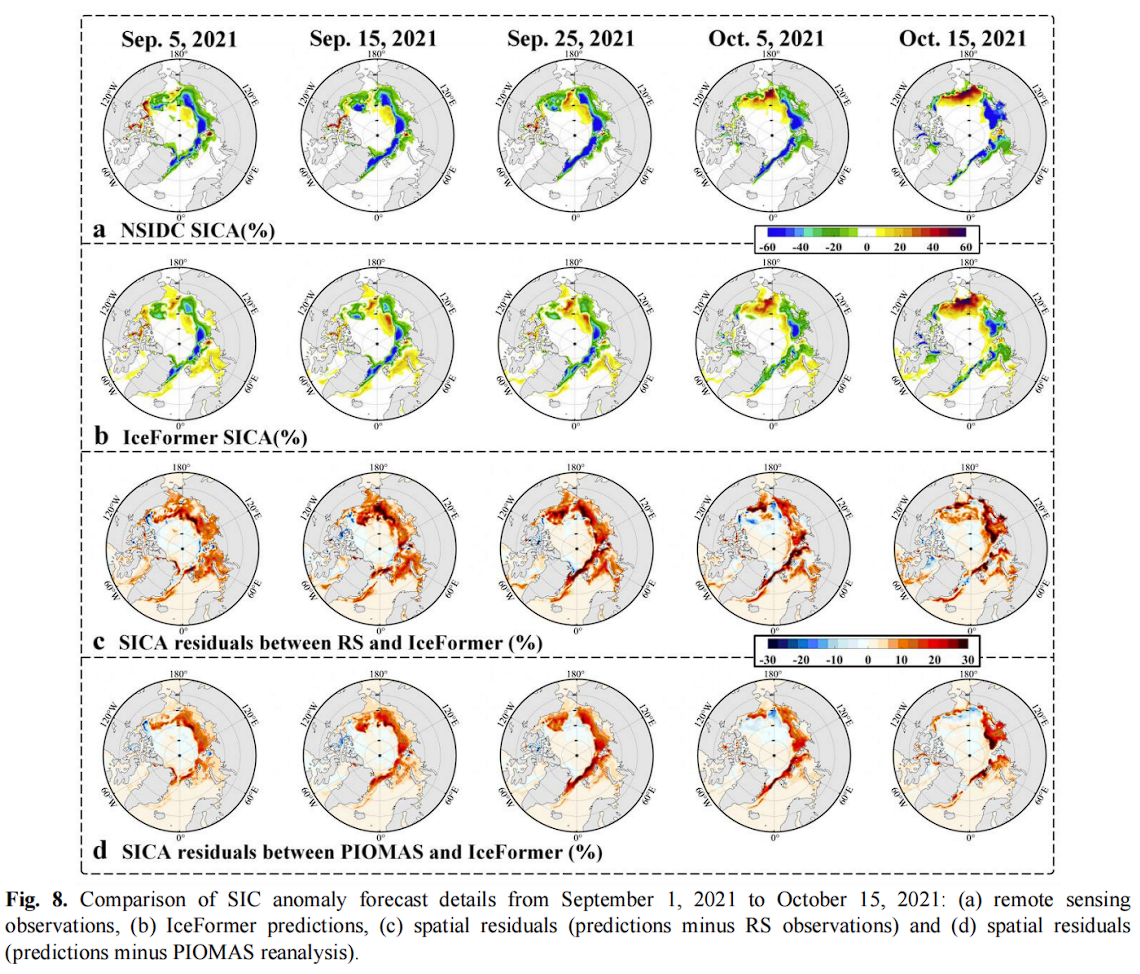
图 8 展示了 SICA 的详细信息。可以看到,IceFormer的预测结果基本与RS观测和PIOMAS再分析结果一致,如图8(a)和(b)所示。总体而言,IceFormer预测结果的异常值分布小于观测值(图8 d),这表明预测结果的不确定性与遥感观测大致相同。
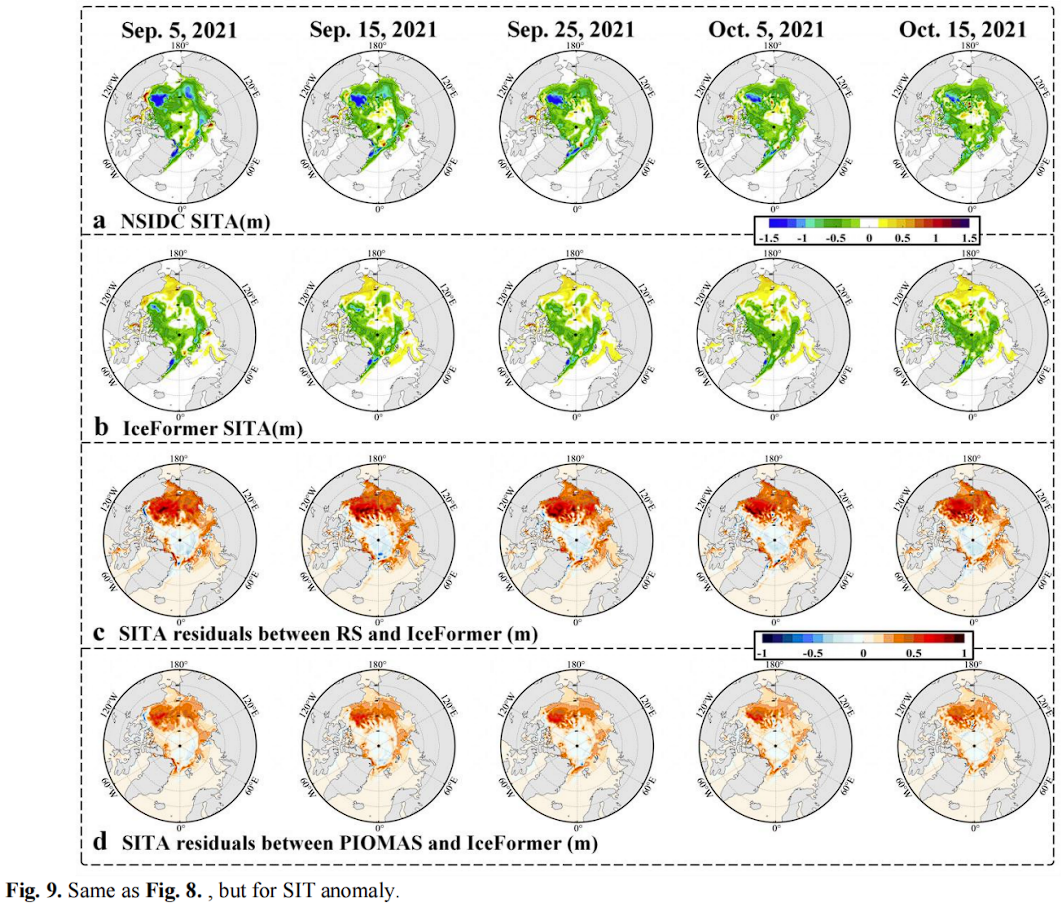
图 9 展示了 SITA 的详细信息。IceFormer的预测结果通常大于遥感观测,如图9(a)和(b)所示。
可以发现IceFormer的预测结果显著高估了北极盆地沿海水域的SIT。
可以从下图看到预测结果高估的原因:

IceFormer的整体预测性能显著优于Persist,但SIE的预测也会向外延伸。这表明IceFormer估计的SIE大于观测值,并存在滞后效应。
上述误差的原因在于两个变量的共同预测中,主要演变集中在大尺度和中尺度,而海冰边缘区域更多地受小尺度控制。此部分的小尺度误差有两个来源:一方面来自主要模态的截断;另一方面,冰融季节的小尺度高频演变强烈非线性。值得一提的是,由于夏季海冰的重新网格化精度仍然不足,数据插值误差也应被视为误差来源。
季节尺度预测的比较
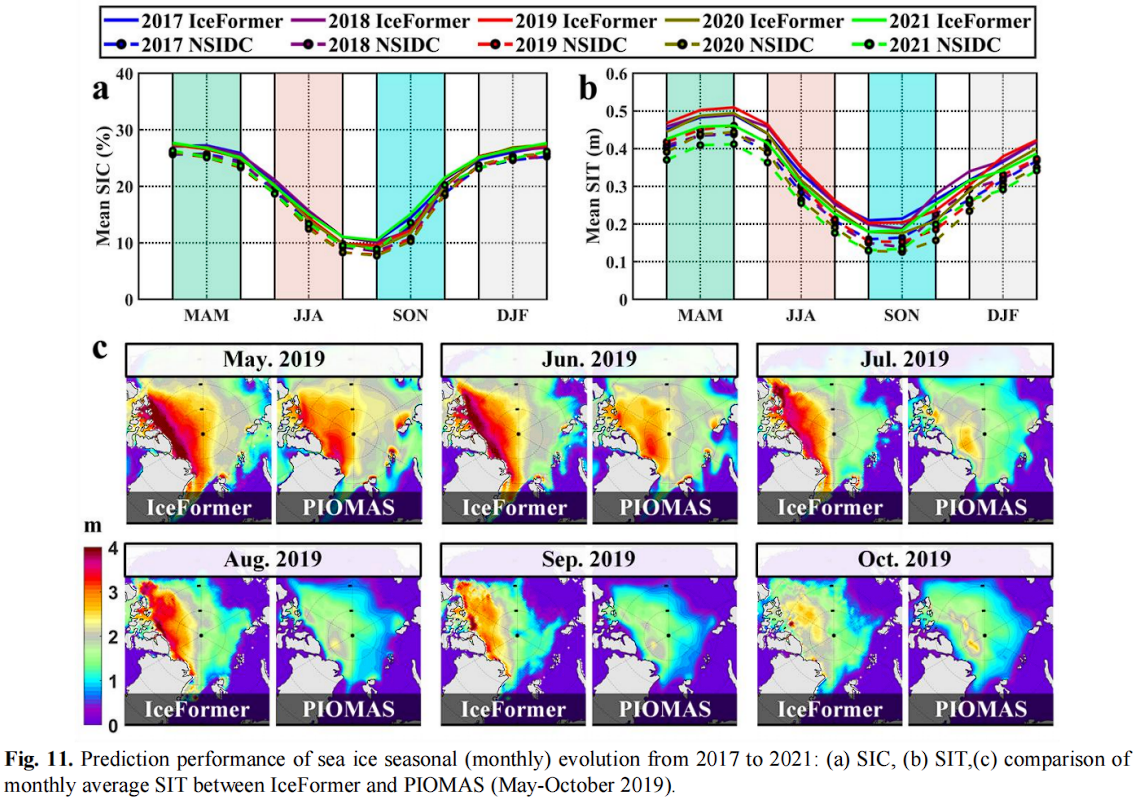
5 年(60 个月)的月度SIC和SIT预测,如图 11 所示。可以看到:IceFormer在整体月度尺度上保持了与观测一致的趋势。
总体而言,IceFormer将相对高估SIC 9%(图11(a))和SIT 13%(图11(b))。从图 11 c 中也可以看出:IceFormer的SIE预测更准确,但SIT显著偏高。
IceFormer的预测结果反映了数据驱动模型对未来海冰含量的稳定高估,这可能是由于我们对长期气候趋势对海冰变化影响的乐观估计所导致的系统不确定性。
总之,IceFormer模型在捕捉季节尺度的海冰演变方面表现良好,其亚季节预测的相对误差在可接受范围内。
同时,季节性海冰的预测也提醒我们,在海冰预测研究中应将气候变化等大规模信号视为直接的误差来源,尤其是在复杂的海洋-大气-海冰耦合系统中。
与其他几种深度学习模型的比较
将 IceFormer 与之前用于海冰浓度(SIC)预测的三种深度学习模型进行对比,比如 Unet, ConvLSTM,融合注意力机制的 UNet。
其结果如下所示:
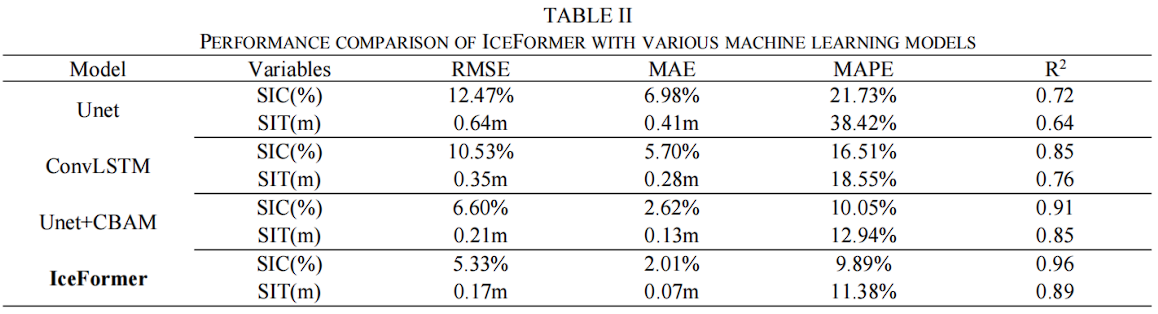
可以看到,IceFormer 在所有的指标上都优于其他的模型。三种基于 CNN 的模型的均方根误差(RMSE)分布大致与 IceFormer 相同,表明每个模型都捕捉到了海冰的时间演变。
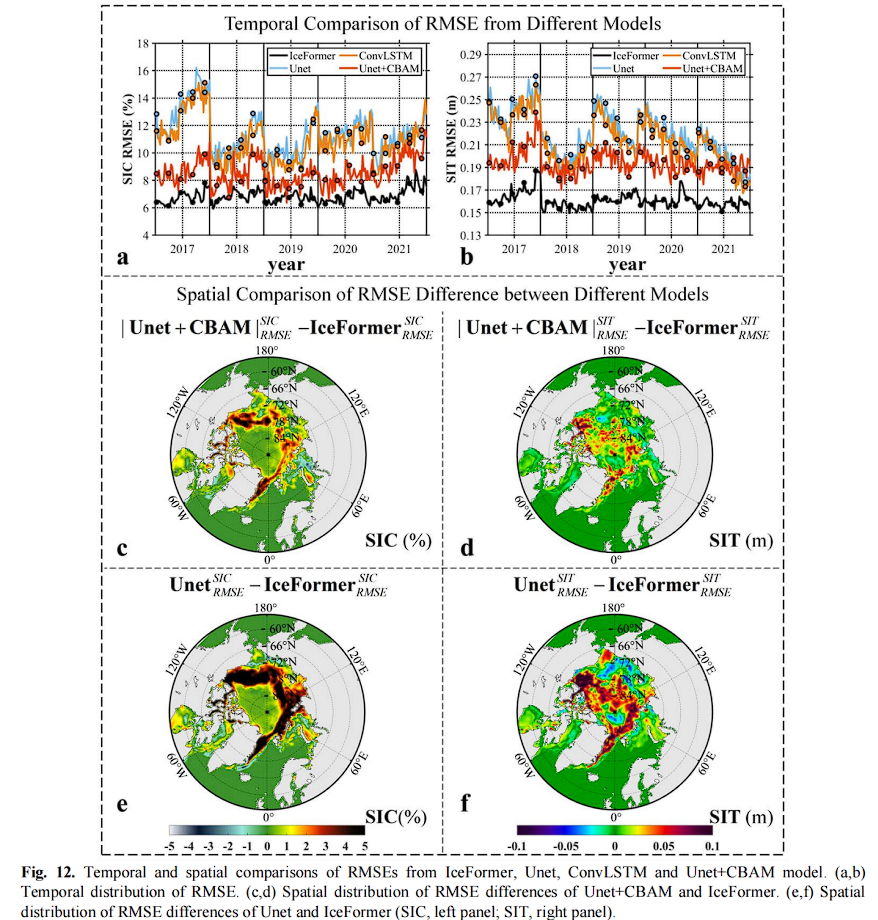
图 12(a) 和 (b) 显示了四种模型的 RMSE 的时间分布。这表明,IceFormer 的总体误差远小于 Unet 和 ConvLSTM,同时,注意力机制能更有效地捕捉 SIC 和 SIT 的非线性演变。
通过 SIC 的 RMSE 空间分布 (图 12(c) 和 (e))可以发现,Unet+CBAM 的预测误差比 Unet 小得多,但仍大于 IceFormer。
讨论
与数据模型的性能比较
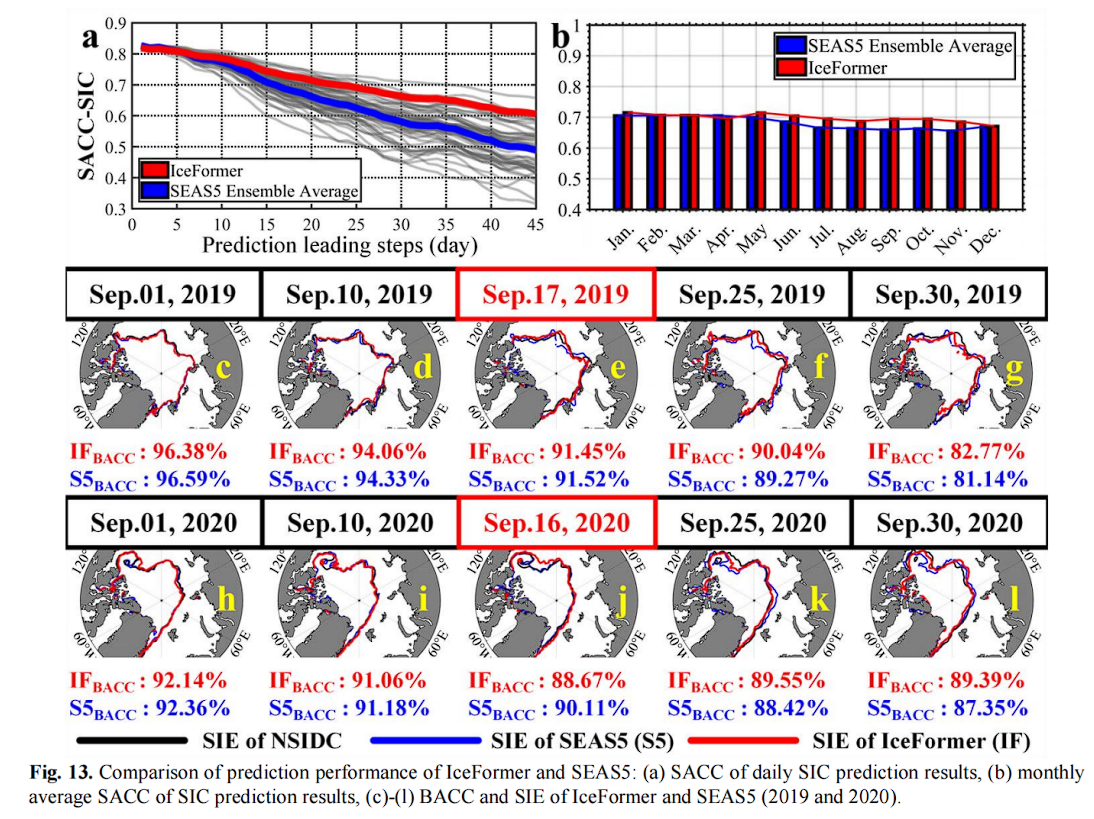
北极海冰预测主要依赖于海冰-海洋耦合数值模型。作者使用SEAS5季节尺度SIC的每日预测进行比较。其结果如图 13 所示。
作者采用 SACC 和 BACC 来评估SEAS5和 IceFormer 在SIC上的预测性能。如图13(a)所示,集合平均SIC的 SACC 在45天的预见期内大于0.5。IceFormer 的 SACC 在15天内与SEAS5相似,但在15天后 IceFormer 的 SACC 高于SEAS5的集合平均。这是因为数值模型的单一输入和输出仅为一个时间步长,这使得误差积累的效果更快且更明显。
如图13(b)所示,IceFormer 和SEAS5对月平均SIC的预测性能大致相同,甚至从5月到11月,IceFormer 的预测性能优于SEAS5。同时,也可以看出,IceFormer 对季节不敏感,具有很强的鲁棒性。
同时,为了验证其稳定性,作者选择了2019年和2020年9月的NSIDC SIC与预测结果进行比较。
其结果如图13(c)-(g)所示,IceFormer 和SEAS5的集合平均预测结果可以有效捕捉2019年9月的海冰融化演变。
以上结果均表明,IceFormer 的预测性能可与以SEAS5为代表的复杂海冰-海洋耦合数值模型相媲美。在某些情况下,其预测结果甚至优于数值模型。
IceFormer 的可预测性与因果机制
作者认为,造成可解释性困难的主要原因是缺乏直接量化的方法来推断变量之间的作用机制和因果关系。
作者采用 Liang-Kleeman 信息流方法来识别变量之间因果关系的方向与大小。
从变量 $X_j$ 到变量 $X_i$ 的传递的绝对速率计算如下:
$$
T_{j \to i} = \frac{1}{\det C} \cdot \sum_{k=1}^{d} \Delta_{jk} C_{k,di} \cdot \frac{C_{ij}}{C_{ii}}
$$
$C$ 是协方差矩阵,$d$ 是变量的数量,$\Delta_{jk}$ 是 $C$ 的余因子,$C_{k,di}$ 是所有 $X_k$ 和 $dX_i/dt$($t$ 为时间)的样本协方差,$C_{ij}$ 是 $X_i$ 和 $X_j$ 之间的样本协方差,$C_{ii}$ 是 $X_i$ 的样本方差。当 $T_{j -> i}$ 在统计上不同于 0 时,$X_j$ 对 $X_i$ 有影响。
分析的数据是 IceFormer 输入的 50 个主要主成分(PCs)。同时,根据每年的时间窗口构建了 32 年的集合样本。通过自助法(bootstrap)重新抽样评估 iceFormer 的不确定性。其结果如下所示
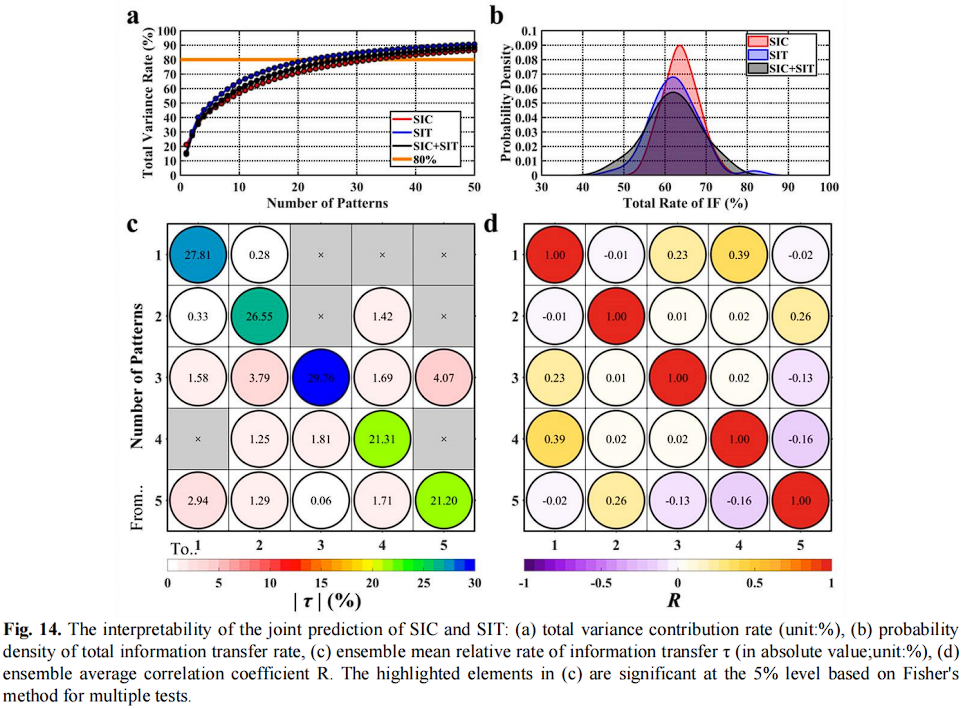
图14(c)和(d)显示了输入数据到IceFormer的总体信息传递平均相对比率和相关系数矩阵(仅显示前5个PCs)。
在当前框架中,自影响意味着可变状态的动态依赖于可变状态本身。除了自影响,不同PCs之间的双向信息传递表明SIC和SIT的某些模式之间存在交互。如图14(a)所示,前5个模式提供了约50%的SIC和SIT的空间演变信息。
除了未通过显著性检验的部分,大多数PCs交换信息且方向不同。例如,从PC3到PC5的信息传递率约为4%,而反向仅为0.06%。这表明从PC3到PC5的信息传递过程更为重要。
其中,PC3和PC5代表不同尺度的演变。这表明北极海冰的不同时间和空间尺度之间存在交互。因此,IceFormer提取海冰联合演变模式的方法是合理的。